Кривая плотность - распределение
Cтраница 1
Кривые плотности распределения р / ( /) представлены на рис. 8.11 при разных значениях параметра сгх с учетом ограничения, налагаемого законом сохранения энергии. [1]
Кривые плотности распределения частиц в тонкой и грубой фракциях построены таким образом, что значения их ординат умножены на их долю в исходном материале. Поэтому обе эти кривые вписываются внутрь кривой плотности распределения частиц исходного материала. [2]
Кривые плотности распределения проницаемости для второго интервала УКПГ-2 месторождения Медвежье. [3]
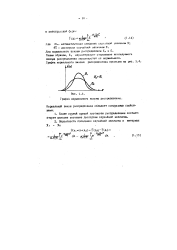 |
График нормального закона распределения. [4] |
Более крутой кривой плотности распределения соответствует меньшее значение дисперсии случайной величины. [5]
Анализ кривых плотностей распределения времени безотказной работы насосов показал, что отказы насосов по причине износа рабочих колес, изготовленных из стали 20Х13Л, начинают появляться уже после IOOO-IIOO часов, в то время как для насосов с рабочими колесами из стали XI7H2I они появляются лишь после 2000 - 3000 часов работы насосов. [6]
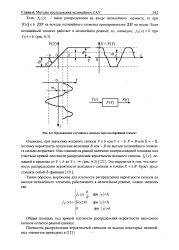 |
Прохождение случайного сигнала через нелинейный элемент. [7] |
Общая площадь под кривой плотности распределения вероятности выходного сигнала остается равной единице. [8]
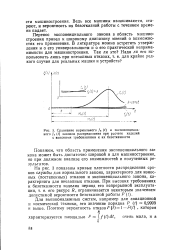 |
Сравнение нормального / н ( 0 и экспоненциального / a ( t законов распределения при расчете изделий с высокими требованиями к их безотказности. [9] |
На рис. 3 показаны кривые плотности распределения сроков службы для нормального закона, характерного для износ-ных ( постепенных) отказов и экспоненциального закона, характерного для внезапных отказов. [10]
На рис. 1 представлены кривые плотности распределения частиц меченого материала по времени пребывания в реакторах кипящего слоя с различной формой горизонтального сечения. [11]
Площадь, заключенная под кривой плотности распределения р ( х), согласно правилу нормирования, равна единице, то есть отражает вероятность всех возможных событий. [12]
Точка на оси х, соответствующая максимуму кривой плотности распределения, называется модой, то есть мода - это наиболее вероятное значение случайной величины. Однако, мода существует не у всех распределений. [13]
График функции р ( х) называется теоретической кривой плотности распределения случайной величины. [14]
Так, например, любой человек, рассматривая кривые плотности распределения, приведенные в табл. 3 - 3, без каких-либо затруднений укажет центры этих распределений. [15]
Страницы: 1 2 3 4