Спектральная плотность

Cтраница 1

Спектральная плотность ( сигначов) АЭ представляет собой распределение сигналов АЭ по частотам энергии. [1]

Спектральная плотность z ( t) связана с корреляционной функцией z ( t) z ( t r) теоремой Винера-Хинчина. [2]

Спектральная плотность существует и ограничена для любого незатухающею ограниченного процесса, ие содержащего гармонических компонент. [3]

Спектральная плотность состоит из непрерывной части и дискретной спектральной линии на нулевой частоте. [4]

Спектральная плотность [ см. ( 12) ] и автокорреляционная функция [ см. ( 8) ] связаны между собой соотношением, играющим очень важную роль. [5]

Спектральная плотность, соответствующая равновесной корреляции плотность - плотность, может быть непосредственно измерена. Мы видели в разд. Последний можно определить, измеряя интенсивность упругого рассеяния электромагнитных волн или нейтронов в жидкости. Если рассматривать неупругое рассеяние, сопровождаемое передачей не только импульса ftk, но и энергии Йсо, то можно определить форм-фактор ak ( со), зависящий как от волнового вектора k, так и от частоты со рассеянного излучения. Со времени работы Ван Хова неупругое рассеяние нейтронов стало мощным орудием экспериментальных исследований динамических, зависящих от времени явлений в жидкостях. [6]

Зависимость дисперсии флуктуации интенсивности плоской волны от параметра Pjj.| Коэффициент пространственной корреляции интенсивности плоской волны.| Временной спектр флуктуации интенсивности плоской волны. [7]

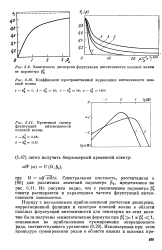
Спектральная плотность, рассчитанная в [86] для различных значений параметра РО, представлена на рис. 6.11. Из рисунка видно, что с увеличением параметра Ро спектр расширяется и характерная частота флуктуации интенсивности повышается. [8]

Спектральная плотность имеет J-образные особенности в идеальных системах, в которых элементарные возбуждения не затухают. В дальнейшем мы будем предполагать, что все интересующие нас динамические переменные являются эргодическими. [9]

Спектральные плотности 5 ( ш) являются простейшими и достаточно информативными количественными характеристиками стохастических движений динамических систем. Измеряя их экспериментально или вычисляя с помощью ЭВМ, можно довольно четко выделять момент начала хаотизации, а также происходящие бифуркации при плавном изменении параметров. [10]

Спектральная плотность может быть получена путем предельного перехода от математического ожидания квадрата модуля текущего спектра при интервале Т, стремящемся к бесконечности. [11]

Спектральная плотность может быть определена как преобразование Фурье корреляционной функции, так и с помощью набора узкополосных фильтров и вычисления средних квадратичных значений выходных величин этих фильтров. [12]

Спектральная плотность ( spectral density) сигнала характеризует распределение энергии или мощности сигнала по диапазону частот. Особую важность это понятие приобретает при рассмотрении фильтрации в системах связи. Мы должны иметь возможность оценить сигнал и шум на выходе фильтра. [13]

Спектральная плотность затем вычисляется как преобразование Фурье автокорреляционной функции. [14]

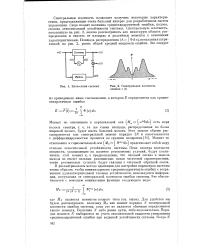Блок-схема системы.| Спектральная плотность ошибки е ( t. [15]

Страницы: 1 2 3 4