Спектральная плотность - возмущение
Cтраница 1
Спектральные плотности возмущений со стороны двигателя и со стороны дороги могут быть найдены при помощи статистической обработки результатов тензометрирования ведущего и ведомого вала зубчатой передачи. [1]
Но в этом случае возможно упрощение - спектральную плотность возмущения можно принять в пределах основной полосы пропускания системы постоянной. [2]
В ходе этого расчета наибольшее время тратится на определение спектральной плотности возмущения на входе. [3]
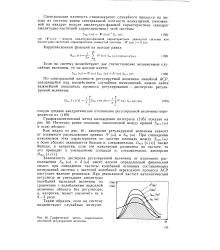 |
Графический метод определения дисперсий регулируемой величины. [4] |
Спектральная плотность стационарного случайного процесса на выходе из системы равна спектральной плотности возмущений, умноженной на квадрат модуля амплитудно-фазовой характеристики ( квадрат амплитудно-частотной характеристики) этой системы. [5]
Так как промышленные САР имеют сравнительно низкие рабочие частоты, то обычно этих трех членов ряда оказывается достаточно для определения спектральной плотности возмущения. [6]
Далее, используя основное соотношение (4.57), находят спектральную плотность случайного процесса на выходе системы, предварительно построив график квадрата модуля амплитудно-фазовой характеристики как функцию частоты, и перемножают ординаты этого графика на значения спектральной плотности возмущения при одинаковых частотах. [7]
При исследовании колебаний упругих систем с распределенными параметрами более осторожно следует относиться к учету взаимной корреляции обобщенных координат. Этим обстоятельством можно пренебречь только в том случае [14], если система не имеет кратных и очень близких частот, затухание системы мало ( система узкополосна) и спектральная плотность возмущения не имеет резких максимумов и разрывов. Поэтому сначала необходимо определить спектр собственных частот системы и в зависимости от его вида решать вопрос об учете взаимной корреляции между формами колебаний. Решение задач методом разложения по формам колебаний сопряжено со значительными трудностями, так как только в некоторых случаях возможно точно определить несколько низших форм и собственных частот колебаний системы. [8]
Дисперсии могут быть вычислены интегрированием в частотной области спектральных плотностей выходных процессов. Если спектральную плотность возмущений аппроксимировать подходящим дробно-рациональным выражением, то можно составить систему линейных алгебраических уравнений, решение которой сразу дает дисперсии и взаимные корреляционные моменты координат без предварительного определения спектральных плотностей. [9]
Точка 6 соответствует началу области перехода, а точки 3 и 1 расположены за областью перехода. Как было указано в разд. При частотах выше верхней границы спектральная плотность возмущений близка к уровню шума аппаратуры термоанемометра. Стрелками на рис. 11.4.5 обозначены рассчитанные с помощью линейной теории устойчивости частоты наиболее неустойчивых колебаний. [10]
Точка 6 соответствует началу области перехода, а точки 3 к 1 расположены за областью перехода. Как было указано в разд. При частотах выше верхней границы спектральная плотность возмущений близка к уровню шума аппаратуры термоанемометра. Стрелками на рис. 11.4.5 обозначены рассчитанные с помощью линейной теории устойчивости частоты наиболее неустойчивых колебаний. [11]
Сила, обеспечивающая собственную устойчивость самолета, подобна упругой восстанавливающей силе. Учитывая три момента инерции по трем осям, получим почти незатухающие резонансные контуры в каждой осн. Возмущающей силой, действующей на самолет по углу тангажа, является ускорение с равномерным спектром в диапазоне между 0 0001 и 1 гц. В чувствительном устройстве, измеряющем угол тангажа, вводится дополнительный белый шум со спектральной плотностью, равной спектральной плотности возмущений от нагрузки при 0 1 гц. Резонансная частота колебаний по углу тангажа равна 0 2 гц. [12]
Страницы: 1