Спектральная плотность - энергия
Cтраница 1
Спектральная плотность энергии в (2.3) и (2.4) рассчитана на единичный интервал волновых чисел. [1]
Спектральная плотность энергии Що, Ь) вычисляется по формуле (3.18), где v ( /) заменяется мгновенными компонентами ( в декартовой системе координат) ускорения электрона x ( t), ij ( t), и проводится интегрирование. [2]
Спектральная плотность энергии альвеновских волн была пропорциональна f - v в-интервале частот 4 - 10 - 2 f 1 4 - 10 - 4 Гц, а показатель v менялся в пределах 1 5 О 2 2, меньшие значения v наблюдались в более горячих потоках плазмы. [3]
Матрица спектральных плотностей энергии имеет следующие свойства. [4]
Отношение спектральных плотностей энергий при двух температурах - измеряемой Т и базовой Т0 равно отношению этих температур для длин волн, больших 1 мм. В качестве базовой выбирают температуру затвердевания золота Го 1337 58 К. [5]
Вычислим спектральную плотность энергии поперечного электрического поля в бесконечной плазме, диэлектрический коэффициент которой Кт не обладает пространственной дисперсией. [6]
Формула для спектральной плотности энергии допускает прямую экспериментальную проверку. Она с высокой точностью подтверждается на опыте, что в настоящее время рассматривается как одно из доказательств правильности основных идей статистической физики и квантовых представлений о природе света. [7]
Что касается спектральной плотности энергии излучения р ( v, Т), то методами термодинамики ее найти не удается, и ее определение представляет задачу статистической физики. Эти сведения составляют содержание закона Вина, к выводу которого мы теперь и приступим. [8]
 |
Модель абсолютно черного тела. [9] |
Задача о спектральной плотности энергии теплового излучения является основной в теории излучения и ее решению посвятили свои усилия многие выдающиеся физики. [10]
Спектр источника, спектральная плотность энергии излучения которого постоянна для всех длин волн видимой области спектра. [11]
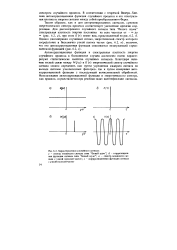 |
Характеристики случайного сигнала. [12] |
Автокорреляционная функция и спектральная плотность энергии случайного процесса в большинстве случаев достаточно полно характеризуют статистические свойства случайных сигналов. [13]
Таким образом, спектральная плотность энергии пуассоновского импульсного процесса состоит из постоянной К и спектральной плотности энергии скоростной функции. Заметим, что из-за наличия постоянной К полная энергия, связанная с процессом U ( t), является бесконечной, даже если K ( t) имеет конечную энергию. [14]
Выражение же для спектральной плотности энергии uv ( v, Т), как и величину постоянной Стефана - Больцмана 0, методами термодинамики найти не удается. [15]
Страницы: 1 2 3 4