Одномерная плотность

Cтраница 1

Одномерная плотность, вероятности недостаточна для полной характеристики случайного процесса, так как она дает вероятностное представление о случайном процессе X ( t) только в отдельные фиксированные моменты времени. [1]

Одномерной плотности распределения для описания шума недостаточно. Однако гармонический анализ к исследованию шума непосредственно применить нельзя ( А. А. Харкевич, 1962), так как спектры Фурье реализаций шума оказываются случайными функциями частоты. [2]

Как определяют одномерную плотность распределения сигнала на выходе нелинейной безынерционной системы. [3]

Мы знаем, что одномерные плотности получаются согласно (5.1.15) интегрированием двумерной плотности по соответствующим переменным. [4]

Следует отметить, что одномерная плотность распределения вероятности неотрицательная величина и площадь под кривой р ( х, ti) равна единице. [5]

В дальнейшем нас будет интересовать главным образом одномерная плотность распределения амплитуды, так как с помощью этой функции определяются необходимые для расчета вероятностные параметры выхода системы. [6]

Плотности распределения большей размерности определяют как произведение одномерных плотностей. [7]

Для этого из двумерной плотности мы должны получить одномерную плотность их отношения. [8]

Стационарность ( в широком смысле) означает, что одномерная плотность распределения ЭПР и ее два первых момента не зависят от начала отсчета времени. [9]

Известно [1-3], что для нормальных линейных СДУ ( 6) одномерная плотность и переходная плотности нормальны и поэтому имеют эллипсоидальную структуру. Поэтому особое внимание уделим точным ( явным) решениям УФПК ( 10), ( 12) для нелинейных СДУ ( 6), обладающим эллипсоидальной структурой. [10]

В отличие от совместной плотности распределения р ( х, у) одномерные плотности р ( х) и рл ( у) называют маргинальными. [11]

При решении задач об определении вероятности разрушения особый интерес представляет случай, когда одномерная плотность распределения процесса и плотность распределения уровня различны. [12]

Марковские процессы ( процессы без последействия), для них многоточечные вероятности выражаются через одномерные плотности распределения и двухточечные плотности вероятности перехода. [13]

Очевидно, что в спектрах СФУР реальных полупроводников содержится смесь пиков, соответствующих процессам с сохранением k и одномерной плотности состояний. Полной ясности в вопросе о том, почему к этим двум семействам полупроводников применимы противоположные модели, не существует. Однако можно предположить, что модель непрямых переходов применима тем лучше, чем большее число одномерных критических точек находится внутри зоны Бриллюэна. [14]

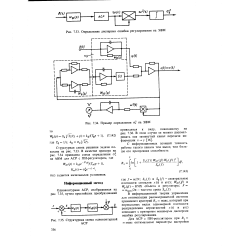Определение дисперсии ошибки регулирования на ЭВМ.| Пример определения of на ЭВМ.| Структурная схема одноконтурной АСР. [15]

Страницы: 1 2 3