Площадь - эпюр
Cтраница 1
Площадь эпюра е равняется зазору между двумя любыми сечениями стержня. [1]
Площадь эпюра Е, построенного для стержня, заделанного своими концами, не имеющего зазоров, должна равняться нулю. [2]
Следовательно, площадь эпюра Qy равняется алгебраической сумме моментов сосредоточенных пар, приложенных к балке с обратным знаком. [3]
Следовательно, взаимные перемещения сечений стержня равны площади эпюра сг между этими сечениями, деленной на Е; для непрерывного стержня с заделанными концами площадь эпюра а равна нулю; при наличии зазора между сечениями стержня площадь эпюра а, деленная на Е, равняется зазору. [4]
Так как в сечении С единичного эпюра - излом, площадь эпюра моментов от заданных сил в этом сечении разбиваем на две части. [5]
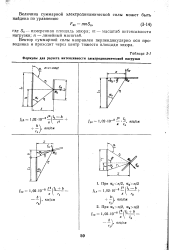 |
Формулы для расчета интенсивности электродинамической нагрузки. [6] |
Вектор суммарной силы направлен перпендикулярно оси проводника и проходит через центр тяжести площади эпюра. [7]
Как следует из вывода правила, в том сечении, в котором имеется излом или скачок в единичном эпюре, площадь эпюра моментов от заданных сил должна разбиваться на две части. Подчеркиваем, что пренебрежение этим приведет к совершенно неверному решению задачи. [8]
Следовательно, взаимные перемещения сечений стержня равны площади эпюра сг между этими сечениями, деленной на Е; для непрерывного стержня с заделанными концами площадь эпюра а равна нулю; при наличии зазора между сечениями стержня площадь эпюра а, деленная на Е, равняется зазору. [9]
Следовательно, взаимные перемещения сечений стержня равны площади эпюра сг между этими сечениями, деленной на Е; для непрерывного стержня с заделанными концами площадь эпюра а равна нулю; при наличии зазора между сечениями стержня площадь эпюра а, деленная на Е, равняется зазору. [10]
Эпюры аксиальной Fz и полной Fs сил представлены на рис. 5.21. В качестве положительного направления Fz принято направление от левого торца индуктора к правому. Площадь эпюра Рг не равна нулю, вследствие чего существует суммарная аксиальная сила, стремящаяся сдвинуть обмотку вправо. Эта сила равна сумме аксиальных сил, действующих на заготовки. На характер распределения полной силы влияют также радиальные силы FR. Эти силы максимальны в зоне немагнитной заготовки, где напряженность Яг примерно в два раза выше, чем в зоне магнитной заготовки. [11]
Знак момента пары совпадает со знаком скачка от нее на эпюре Мг. Таким образом, изгибающий момент в сечении равняется части площади эпюра Qy, сложенной с алгебраической суммой моментов сосредоточенных пар по одну сторону от сечения. [12]
Страницы: 1