Поверхность - ток
Cтраница 1
Поверхности тока определяются как поверхности, на которых значение функции ф является постоянным, они параллельны вектору скорости v в каждой точке. Напомним, что пересечение поверхности тока с плоскостью, содержащей ось симметрии, называется линией тока. Как известно, физический смысл функции тока заключается в том, что величина 2тгф в любой точке определяет мгновенный объемный расход жидкости. [1]
 |
Линия тока ( штриховая линия. [2] |
Поверхность тока - поверхность, образованная линиями тока, которые проходят через все точки заданной в пространстве неподвижной линии. [3]
Поверхность тока - поверхность для фиксированного момента времени, в каждой точке которой вектор скорости лежит в касательной плоскости. [4]
 |
Линия тока ( штриховая линия. [5] |
Поверхность тока - поверхность, образованная линиями тока, которые проходят через все точки заданной в пространстве неподвижной линии. [6]
Поверхности тока должны пересекать эту плоскость под прямым углом. [7]
Поверхности тока поля (1.121) образуются, например, вращением кривых R ( 0) вокруг оси диполя. [8]
Вдоль поверхности тока предполагается изоэнтропийный закон изменения плотности, хотя для различных поверхностей тока давление торможения в общем случае может быть и различным. [9]
Условимся поверхность тока называть вогнутой, если нормаль к ее образующей направлена от оси машины, и выпуклой, если нормаль направлена к оси машины. [10]
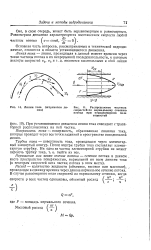
Воображают поверхности тока, которыми вся турбина разбивается на частичные ( элементарные) турбины, пропускающие равные расходы. Меридиональные сечения этих поверхностей проводят на намеченном профиле в виде линий / / и / / / на фиг. Сечения поверхностей тока / и IV совпадают с очертаниями ободьев колеса. [11]
 |
Меридиональное сечение проточной части турбины.| Меридиональное сечение осесимметричной поверхности тока с основными обозначениями. [12] |
Выбрав близкие поверхности тока, приходим к задаче обтекания аэродинамической решетки, расположенной на поверхности вращения в слое переменной толщины. [13]
Пересечения поверхностей тока могут быть названы линиями потока. Если единица выбрана достаточно малой, число линий потока, пересекающих некоторую поверхность, примерно равно числу пересекающих ее потоковых трубок, и мы, таким образом, можем рассматривать линии потока как определяющие не только направление тока, но также и его силу, поскольку каждая линия потока, пересекающая данную поверхность, соответствует единичному току. [14]
В эти поверхности тока входят также сама сфера и ось симметрии, которые разделяют течение. Соображения о разделяющей линии тока дают тогда нам возможность построить общую форму линий тока в меридиональной плоскости ( рис. 330); линии тока здесь стягиваются вокруг критических точек. [15]
Страницы: 1 2 3 4