Качественный анализ - уравнение
Cтраница 1
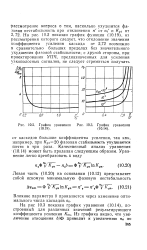 |
График уравнения [ IMAGE ] График уравнения.. [1] |
Качественный анализ уравнения (10.14) может быть проделан следующим образом. [2]
Такое преобразование полезно для качественного анализа уравнения и при использовании приближенных методов решения. [3]
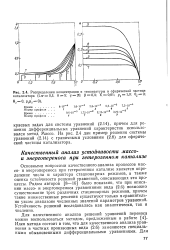 |
Распределения концентрации и температуры в сферической частице катализатора ( Lw 0 l. 6 5. v 20. Р 0 4. К 0 01. yl fl В. 0. [4] |
Идея метода состоит в том, что для качественного анализа уравнения в частных производных вида (2.6) заменяются специальными обыкновенными дифференциальными уравнениями. [5]
Ниже мы рассмотрим некоторые пути интерпретации плохо разрешенных спектров, основанные на качественном анализе уравнений, описывающих суммарный спектр ЭПР, и покажем на наиболее простых примерах, какие сильные искажения спектра могут иметь место вследствие указанных выше причин. При этом мы дадим ряд формул и приемов анализа, которые могут быть применены при рассмотрении спектров таких типов. Эти методы весьма просты, и их можно применять в принципе и к другим более сложным спектрам. Однако большая трудоемкость расчетов сильно осложняет предложений путь анализа. Поэтому в следующем параграфе мы приведем результаты, полученные в последнее время в Институте химической физики АН СССР по использованию для этих расчетов быстродействующей электронно-счетной машины. [6]
Факты существования и направления силы в системах с одной обмоткой возбуждения могут быть установлены через качественный анализ уравнений силы. Вообще говоря, сила всегда направлена так, чтобы увеличивать индуктивность или уменьшать магнитное сопротивление в магнитных системах и чтобы увеличивать емкость в электростатических системах. [7]
Основным отличием от первых конференций и особенностью 1У конференции является применение теории сложных систем к исследованию химических процессов и реакторов, построение и исследова - ние сложных систем на основе ступенчатого иерархического построения их моделей, исследование многофазных процессов. На конфе - ренции оформилась также новая область в моделировании химических процессов - математические вопросы моделирования химических реакторов, которая состоит из пяти разделов: обработка кинетичес - ких данных и планирование эксперимента; качественный анализ уравнений математического описания с целью определения числа стационарных режимов, их устойчивости и чувствительности; оптимиза - ция процессов и реакторов; численные методы решения на ЭВМ; математическое обеспечение и средства математического моделирова - ния. [8]
Для изученных в [187, 188] систем спиновые представления кристаллографических групп имеют высокую размерность и несколько инвариантов четвертого порядка. Качественный анализ уравнений ренормгруппы показывает, что, как правило, стабильные неподвижные точки вообще отсутствуют, так что фазовый переход совершается скачком. Однако для некоторых кристаллографических групп фазовый переход второго рода не запрещен. [9]
Определив из (2.5.11) и остальных s уравнений медленных нестационарных процессов медленные переменные и внеся результат в выражения для быстрых переменных, получим полное решение задачи (2.5.11) в первом приближении. Очевидно, что такой путь существенно проще непосредственного интегрирования исходной системы. Вследствие этого облегчается качественный анализ уравнений нестационарных процессов. [10]
Аналитические аппроксимации связаны в основном с построением линейных моделей, не учитывают нелинейности и, как правило, достаточно просты и физически наглядны, но приближенны. Это противоречие разрешается лишь совместным использованием методов качественного анализа уравнений химической кинетики и численного моделирования. [11]
Рассматривая возможность обобщения задачи и анализа качественных закономерностей, инженеру приходится считаться с перспективой возрастания объема работы. Однако логика погружения не обязательно ведет к увеличению количества вычислений. Например, если известно общее решение дифференциального уравнения, то анализ поведения системы во всей области допустимых граничных условий оказывается не более трудным, чем расчет конкретной траектории. В этом смысле методы аналитического решения и качественного анализа уравнений выигрывают по сравнению с прямым численным методом. [12]
Рассматривая возможность обобщения задачи и анализа качественных закономерностей, инженеру приходится считаться с перспективой возрастания объема работы. Однако логика погружения не обязательно ведет к увеличению количества вычислений. Например, если известно общее решение дифференциального уравнения, то анализ поведения системы во всей области допустимых граничных условий оказывается не более трудным, чем расчет конкретной траектории. В этом смысле методы аналитического решения и качественного анализа уравнений выигрывают по сравнению с прямым численным методом. [13]
Страницы: 1