Боковая поверхность - стержень
Cтраница 2
 |
Теплопередача через стержень. [16] |
Теплота с боковой поверхности стержня, а также с торцовой поверхности противоположного конца отводится в окружающую среду с неизменной температурой ТжТо, коэффициент теплоотдачи на боковой поверхности а, на торцовой а. Требуется рассчитать распределение температуры в стержне и определить тепловой поток Q, передаваемый через стержень в окружающую среду. [17]
Будем предполагать что боковая поверхность стержня теплонепроницаема и что во всех точках поперечного сечения стержня температура одинакова. [18]
 |
Эпюра касательных напряжений, возникающих в поперечном сечении. [19] |
В действительности же боковая поверхность стержня свободна от всяких напряжений, а поэтому и составляющая - с. Следовательно, касательные напряжения в круглом сечении направлены перпендикулярно радиусам. [20]
Будем предполагать, что боковая поверхность стержня теплонепроницаема и что во всех точках поперечного сечения стержня температура одинакова. [21]
Будем предполагать, что боковая поверхность стержня теплонепроницаема и что во всех точках поперечного сечения стержня температура одинакова. [22]
Рассмотрим граничные условия на боковой поверхности стержня. Первые два условия яз уравнений ( 1) на основании равенства ( 4) удовлетворяются тождественно. [23]
Температура среды, окружающая боковую поверхность стержня, принимается постоянной и равной начальной температуре его. [24]
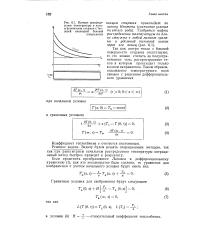 |
Кривые распреде - концом стержня происходит по ления температуры в полу - закону Ньютона ( граничное условие. [25] |
Так как потери тепла с боковой поверхности стержня отсутствуют, то его можно считать за полуограниченное тело, распространение тепла в котором происходит только в одном направлении. [26]
При отсутствии тепловых потерь с боковой поверхности стержня формула ( 4 - 37) переходит в зависимость, полученную Кольраушем. Таким образом, для определения Л необходимо знать р, / и распределение температуры по длине исследуемых стержневых образцов. На рис. 4 - 18 представлена схема опытной установки. Нижний зажим охлаждается змеевиковым холодильником, позволяющим компенсировать тепловое расширение. Измерение падения напряжения на образце осуществляется подвижным штоком 6, который подводит к образцу два щупа 5 с определенным расстоянием между ними. Сила тока и напряжение измеряются компенсационным методом с помощью потенциометра переменного тока. [27]
Перейдем теперь к условиям на боковой поверхности стержня, где должны отсутствовать внешние поверхностные силы. [28]
При этом достигается равномерное срабатывание боковой поверхности стержня крана и сохраняется плотность соединения. [29]
Очевидно, что условия [117] для боковых поверхностей стержня, свободных о г внешних сил, удовлетворяются, так как все составляющие напряжения, за исключением axt равны нулю. [30]
Страницы: 1 2 3 4