Статистическая поверхность
Cтраница 1
Статистические поверхности могут представляться посредством плотности точек, хороплет, дасиметрии и изолиний. Первые три чаще всего имеют дело с дискретными поверхностями, и мы их пока отложим. [1]
Понимание статистических поверхностей этих двух типов может оказаться сложным, поэтому мы рассмотрим их по отдельности. [2]
Определение статистической поверхности как непрерывной означает, что имеется бесконечное количество точек, в каждой из которых может быть свое значение. Однако, провести измерения в бесконечном числе точек - физически невозможно, также как невозможно хранить бесконечный объем данных. Поэтому определение непрерывной поверхности с помощью бесконечного числа точек должно быть заменено моделью, которая использует существенно важные отсчеты ( samples) рассматриваемой величины. Эти отсчеты представляют наиболее важные изменения поверхности как упрощенное представление. [3]
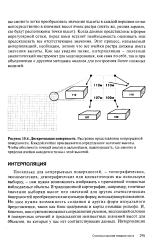
На рис. 6.7 представлены две статистические поверхности и показаны направления их наибольших скатов. Такие приближенные вычисления особенно удобны при сравнении изолинейных карт. [4]
Как было сказано в начале главы, статистические поверхности могут представляться четырьмя различными способами. [5]
Как зависит коэффициент корреляции от угла между направлениями наибольших скатов ( градиентов) двух сравниваемых статистических поверхностей. [6]
Он может применяться к числовым данным, существующим в виде статистической поверхности. Этот метод позволяет улучшить качество количественных данных полигонального покрытия посредством сравнения с более подробными данными другого покрытия. [7]
Поскольку для непрерывных поверхностей, - топографических, экономических, демографических или климатических мы используем выборку, - нам нужна возможность изображать с приемлемой точностью наблюдаемые объекты. В традиционной картографии, например, точечные значения выборки высот или значений для других статистических поверхностей преобразуются в визуальную форму, использующую изолинии. Но нам нужна возможность создания и других форм визуального представления, таких как блок-диаграммы и карты отмывки рельефа. И, конечно, нам нужна возможность определения уклонов, экспозиций склонов и поперечных сечений и предсказания неизвестных значений высот для объектов, на которые у нас нет соответствующих данных. [9]
Пространственное распределение это расстановка, порядок, концентрация или рассеянность, соединенность или бессвязность многих объектов в пределах заключающего их географического пространства. До сих пор рассматриваемые нами методы имели дело главным образом с отдельными объектами или наборами объектов, когда они могли быть определены как регионы, окрестности или представлены как статистические поверхности. Мы лишь очень кратко касались взаимодействия объектов, регионов, поверхностей и окрестностей с аналогичными объектами других покрытий. Но большинство объектов, встречающихся в одном покрытии тоже имеют определимые характеристики пространственного расположения, которые могут указывать на механизмы их возникновения. [10]
Пространственное распределение это расстановка, порядок, концентрация или рассеянность, соединенность или бессвязность многих объектов в пределах заключающего их геофафического пространства. До сих пор рассматриваемые нами методы имели дело главным образом с отдельными объектами или наборами объектов, когда они могли быть определены как регионы, окрестности или представлены как статистические поверхности. Мы лишь очень кратко касались взаимодействия объектов, регионов, поверхностей и окрестностей с аналогичными объектами других покрытий. Но большинство объектов, встречающихся в одном покрытии тоже имеют определимые характеристики пространственного расположения, которые могут указывать на механизмы их возникновения. [11]
Как было сказано в начале главы, статистические поверхности могут представляться четырьмя различными способами. Но данные статистических поверхностей могут также встречаться как дискретные объекты. Для них мы должны рассмотреть некоторые дополнительные методы, как отображения, так и анализа. [12]
Сложение - не единственная математическая операция, которая может использоваться для комбинирования покрытий, могут также использоваться вычитание, умножение, деление, возведение в степень, выбор большего или меньшего значения, усреднение и другие операции. Понятно, что большинство из них требует применения компьютера. Кроме того, существует набор методов для комбинирования покрытий на основе математических операций над покрытиями, действующими как статистические поверхности. Мы их рассмотрим несколько позже. [13]
Как показывает опыт, в напряженном газовом факеле реакции горения локализуются в узких зонах, поперечный размер которых весьма мал по сравнению с размером факела. Иными словами, турбулентный газовый факел представляет собой область интенсивного перемешивания исходных и конечных компонентов, внутри которой в непосредственной близости к средней статистической поверхности максимальной температуры осуществляются химические реакции горения. [14]
В некоторых случаях представляют интерес расстояния и группировки отдельных точечных распределений. Большинство ГИС не очень-то приспособлены для выполнения такого анализа, но это мы рассмотрим уже в следующей главе. Иногда мы также обнаруживаем, что каждая точка сопровождается дополнительными данными, записанными в любой из четырех шкал измерения. Но в контексте статистической поверхности мы обращаем внимание только нате, которые представлены в числовых шкалах. Если мы можем принять, что имеется непрерывность для таких величин, как массы птиц или размеры стай млекопитающих, представленные отдельными точками, то сможем выполнять операции с этими точечными данными, как если бы они были точечной выборкой топографической поверхности, особенно если они записаны в шкале интервалов или отношений. Все же, предположение непрерывности в большинстве из этих случаев неверно, и нам придется рассматривать и сравнивать эти дискретные события по отдельности, либо статистически, либо через сравнения их пространственных отношений. Этот тип анализа мы рассмотрим опять же в следующей главе. [15]
Страницы: 1 2