Начальная поверхность - текучесть
Cтраница 1
Начальная поверхность текучести при различных температурах деформирования первоначально изотропных материалов достаточно хорошо описывается сферой Мизеса с радиусом, зависящим от температуры. [1]
Начальная поверхность текучести описывается поверхностью Мизеса. [2]
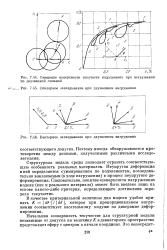 |
Смещение поверхности текучести подэлемента при нагружении по двузвенной ломаной.| Скалярное запаздывание при двузвенном нагружении.| Векторное запаздывание при двузвенном нагружении. [3] |
Начальная поверхность текучести для структурной модели независимо от допуска на величину К в девиаторном пространстве представляет сферу с центром в начале координат. [4]
Начальная поверхность текучести изотропного материала в де-виаторном пространстве представляет сферу с центром в начале координат; ее радиус тем больше, чем больше принятый допуск. Для опытного определения изменения этой поверхности после пластического деформирования приходится использовать партию образцов. Схема испытания одного образца ( для случая двумерного девиаторного пространства) поясняется на рис. 4.10: вначале на-гружение по лучу ОА и разгрузка по АВ ( этот этап одинаков у всех образцов партии), затем вторичное нагружение по лучу, определяемому углом гр, до достижения принятым критерием перехода к пластическому состоянию величины, установленной допуском. Соответствующая точка девиаторной плоскости принадлежит поверхности нагружения. Изменяя ( для разных образцов) значение з, получают всю поверхность. [5]
Согласно постулату изотропии начальная поверхность текучести в 25 является сферой. [6]
При выходе изображающей точки за пределы начальной поверхности текучести развиваются пластические деформации и поверхность текучести при этом деформируется. [7]
В этом легко убедиться, рассмотрев изотропно упрочняющийся материал, начальная поверхность текучести которого не совпадает с поверхностью текучести Мизеса. [8]
Большое значение имеют экспериментальные работы, направленные на исследование формы начальной поверхности текучести и ее трансформации в процессе пластического деформирования материала. [9]
Поэтому в [22] теория течения была модернизирована таким образом, чтобы начальная поверхность текучести имела форму Мизеса - Шлейхера. Вся теория необратимого деформирования поликристаллов, изложенная выше, может быть также легко распространена и на общий случай задания направляющего тензора А / / в шестимерном тензорном пространстве. [10]
Относительно точки М ( путей МТ и ТМ) будем предполагать, что она лежит не только внутри начальной поверхности текучести FK - const, но и внутри новой поверхности текучести для точки Р, т.е. Fp const. Это - существенное предположение, не позволяющее точку М выбирать как угодно близко к начальной поверхности F const. [11]
При Н ф 0 определяющие уравнения предлагаемой теории также являются уравнениями типа теории течения. В этом случае начальная поверхность текучести, представляющая в шестимерном пространстве напряжений Xi сферу радиуса К, в процессе пластического деформирования перемещается как жесткое целое, причем перемещение центра сферы пропорционально вектору остаточной ( пластической) деформации. Закон упрочнения, при котором начальная поверхность текучести испытывает перенос, сохраняя при этом свои размеры и форму, принято называть трансляционным упрочнением. Модель трансляционного упрочнения, аналогичная рассматриваемой в настоящей работе, была независимо несколько позднее предложена Прагером [82] для поверхности текучести общего вида. [12]
Общий вьюод, который следует из анализа экспериментальных данных, состоит в том, что начальные поверхности текучести располагаются, как правило, между поверхностями Мизеса и Треска ближе к поверхности Мизеса, а во многих случаях описываются условием Мизеса с точностью до разброса экспериментальных данных. [13]
При продолжении процесса нагружения за пределом текучести у конструкционных материалов, как правило, увеличивается сопротивляемость пластическому деформированию. Для материалов с выраженным пределом текучести упрочнение характеризуется изменением как размеров, так и положения начальной поверхности текучести в пространстве напряжений. Последующие поверхности текучести, которые образуются в процессе натружения и отделяют области упругого и пластического деформирования друг от друга, называют поверхностями нагружения. [14]
При Н ф 0 определяющие уравнения предлагаемой теории также являются уравнениями типа теории течения. В этом случае начальная поверхность текучести, представляющая в шестимерном пространстве напряжений Xi сферу радиуса К, в процессе пластического деформирования перемещается как жесткое целое, причем перемещение центра сферы пропорционально вектору остаточной ( пластической) деформации. Закон упрочнения, при котором начальная поверхность текучести испытывает перенос, сохраняя при этом свои размеры и форму, принято называть трансляционным упрочнением. Модель трансляционного упрочнения, аналогичная рассматриваемой в настоящей работе, была независимо несколько позднее предложена Прагером [82] для поверхности текучести общего вида. [15]
Страницы: 1 2