Срединная поверхность - стержень
Cтраница 1
Срединная поверхность стержня не претерпевает сдвигов. [1]
 |
Стесненное кручение ределение сдвига в срединной стержня. [2] |
В срединной поверхности стержня отсутствует деформация сдвига. [3]
Вычислим касательную силу S в срединной поверхности стержня. [4]
Введем систему гауссовых координат s, z на срединной поверхности стержня, причем линии г направлены вдоль оси стержня, а линии s лежат в плоскостях поперечных его сечений. [5]
Продольную составляющую смещения точки k определим на основании второй гипотезы об отсутствии сдвигов на срединной поверхности стержня. Для этой цели выделим на срединной поверхности вокруг точки k элементарный квадрат, сторона которого равна элементу дуги ds kkj. [6]
Последнее по толщине стенки распределяется по линейному закону и в точках на средней линии сечения равно нулю, так что срединная поверхность стержня свободна от сдвигов, вызываемых касательными напряжениями тк. [7]
Напряжения т по толщине профиля распределены равномерно ( рис. 8, б) и на средней линии сечения в отличие от напряжений т0 в нуль не обращаются. Этими напряжениями определяются деформации сдвига срединной поверхности стержня, которыми в теории В. [8]
Расстояние между поверхностями f называется текущей толщиной. Геометрическое место средин толщин называется срединной поверхностью стержня, которой он иногда задается. Линия пересечения срединной поверхности с поперечным сечением называется его средней линией. [9]
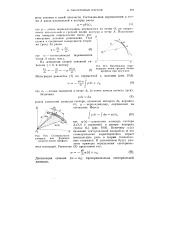 |
Касательное перемещение точки средней линии профиля при кручении. [10] |
Положение оси поворота определяется после рассмотрения условий равновесия. Угол сдвига в срединной поверхности стержня ( разд. [11]
Касательные напряжения, вызываемые действием поперечных сил, в точках на средней л-инии сечения не равны нулю. Поэтому расчеты тонкостенных стержней с учетом изгибно-крутильных деформаций можно производить в предположении, что срединная поверхность стержня свободна от сдвигов. [12]
Рассмотрим тонкостенный стержень открытого профиля, нагруженный по боковой поверхности непрерывно распределенной нагрузкой. На торцах стержня заданы внешние силы или какие-либо условия закрепления. Боковые кромки стержня для простоты считаем свободными. Будем пользоваться системой координат п, s, z, в которой п - расстояние по нормали к срединной поверхности стержня, s - длина дуги срединной линии профиля, z - расстояние по образующей стержня; начало координат поместим в плоскости левого торца. [13]
Страницы: 1