Поворот - радиус
Cтраница 1
Поворот радиуса ОМ с изменением угла В - 9 ( t), при котором движется система координат ( ер, е), определяет переносное движение точки. [1]
 |
График для определения. [2] |
Тогда поворот радиуса R на угол в 360 соответствует времени в - 1 / 0 25 - 106 4 - 1Q - 6 сек. [3]
При повороте радиуса ОА на угол ос получим радиус 05 ( рис. 104), тот же радиус получится и при повороте ОА на угол, отличающийся от а на любое целое число оборотов. [4]
Полотно дороги на повороте радиуса R наклонено в сторону центра закругления и составляет угол а с горизонтом. По дороге едет велосипедист, скорость которого такова, что на повороте велосипед перпендикулярен к полотну дороги. С какой силой F велосипед давит на дорогу, если масса велосипедиста с велосипедом равна ml Какова при этом скорость v велосипеда. [5]
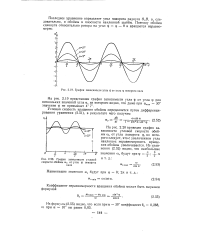 |
График зависимости угла t [ i от угла ф поворота вала.| График зависимости угловой. [6] |
Последнее уравнение определяет угол поворота радиуса ОгВ, а, следовательно, и обоймы в плоскости наклонной шайбы. Поэтому обойма сдвинута относительно ротора на угол ij; р - 6 и вращается неравномерно. [7]
Обычно в масс-спектрометрах угол поворота радиуса ионов 60; это упрощает изготовление электромагнита. [8]
Конец дуги размещается так, чтобы поворот радиуса, пртк1 - денного в начало дуги, на заданный угол происходил в положительном напри. [9]
КО, причем радиус OR получается поворотом радиуса ОР на прямой угол по часовой стрелке. [10]
Колесо вращается так, что зависимость угла поворота радиуса колеса от времени дается уравне -; нием ФA Bt Ct2 Dt3, где В рад. [11]
Изменение положения тела при движении по окружности характеризуют углом поворота радиуса, проведенного к телу. [12]
При движении точки по окружности часто удобно характеризовать ее движение углом поворота радиуса, соединяющего движущуюся точку с центром окружности. Измененце этого угла с течением времени характеризуют угловой скоростью. [13]
 |
Сбрасывание бомбы с пикирующего бомбардировщика. [14] |
При движении точки по окружности часто удобно характеризовать ее движение углом поворота радиуса, соединяющего движущуюся точку с центром окружности. Изменение этого угла с течением времени характеризуют угловой скоростью. [15]
Страницы: 1 2 3