Сравнительный анализ - результат - расчет
Cтраница 1
Сравнительный анализ результатов расчета по предложенной модели показывает, что она адекватно описьгаает экспериментальные данные, полученные в достаточно широком диапазоне начальных условий. [1]
Проведем небольшой сравнительный анализ результатов расчета, получаемых по формулам ( 17 - 6) и ( 17 - 17), исходя из предположения, что излучение среды является селективным. [2]
В настоящей монографии сравнительному анализу результатов расчета слоистых оболочек и пластин на прочность и устойчивость уделяется значительное внимание. [3]
Основная цель теоретических исследований заключается в том, чтобы на основе сравнительного анализа результатов расчета в широких диапазонах изменения геометрических и физических характеристик изотропного упругого диска понять явление толщинного резонанса в упругой пластине конечных размеров. [4]
Выбор условий вакуумной перегонки мазута с получением 50 - 60-градусных фракций произведен путем сравнительного анализа результатов расчета различных схем перегонки на ЭВМ. Выбраны технологический режим и конструкция ректификационного оборудования, обеспе-чивапцие заданную четкость ректификации продуктов вакуумной перегонки мазута, промышленной установки большой единичной мощности. [5]
В этом параграфе дано решение задачи о собственных колебаниях слоистой армированной круговой конической усеченной жестко защемленной оболочки. Выполнен сравнительный анализ результатов расчета, полученных с использованием классических и неклассических дифференциальных уравнений динамики слоистых оболочек, что позволило выявить и оценить влияние поперечных сдвиговых деформаций на собственные частоты и формы колебаний. [6]
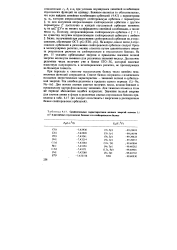 |
Сравнительные характеристики полных энергий атомов Li и F в различных гауссовских базисах и в слейтеровском базисе. [7] |
На вопрос, какое число р-гаус-совских орбиталей в разложении слейтеровской орбитали следует брать в молекулярных расчетах, можно ответить путем сравнительного анализа результатов расчетов на слейтеровском и гауссовском базисах. Достаточно разумные числа получают уже в базисе STO - 3G, который завоевал известную популярность в неэмпирических расчетах, не претендующих на большую точность. [8]
Многими исследователями отмечалось ( например, [147]), что разработка таких методов идет гораздо медленнее, чем создание новых моделей оболочек. Отметим, наконец, что ( оправданное и неизбежное) появление многих уточненных вариантов уравнений выдвигает как одну из актуальных задачу определения границ их применимости. В ее решение должен включаться, в частности, сравнительный анализ результатов расчета слоистых оболочек на основе различных вариантов неклассических уравнений как между собой, так и с решениями на основе уравнений пространственной задачи теории упругости, а также с экспериментальными данными. Разнообразные сравнительные данные позволят выявить характер и степень влияния трансвер-сальных деформаций, уточнить границы пригодности прикладных двумерных уравнений и в их рамках указать наиболее простые и в то же время достаточно точные подходы к анализу слоистых оболочечных систем. [9]
На основе рассматриваемых вариантов уравнений решены многие важные прикладные задачи прочности, устойчивости, динамики, оптимизации слоистых композитных пластин и оболочек. Некоторые из вариантов таких уравнений приведены в параграфе 3.7 настоящей монографии. Там же даны уравнения, составленные Л.П. Хорошуном [316] на основе концепции об однородном напряженном состоянии тонкостенного элемента слоистой структуры. Сравнительный анализ результатов расчета слоистых оболочек и пластин, полученных с использованием различных вариантов двумерных уточненных уравнений, выполнен в работах А.Н. Андреева [13-15], А.Г. Бондаря и А.О. Рассказова [53], Я.М. Григоренко и А.Т. Василенко [120], Г.М. Куликова [162], И.Ю. Патлашен-ко [223], В.К. Присяжнюка и В.Г. Пискунова [246], А.С. Сахарова и др. [273], Н.Г. Сипетовой [277], B.C. Сипетова и О.Н. Демчука [276], A. Noisera и J.N. Reddy [361], J.G. Rena [368] и др. Такие исследования важны - наличие широкого круга сравнительных данных позволит выявить характер и степень влияния поперечных сдвиговых деформаций и обжатия нормали, уточнить границы применимости прикладных уточненных теорий и в их рамках указать наиболее простые и в то же время достаточно точные подходы к анализу слоистых оболочечных систем. [10]
Рассматриваемое направление в механике многослойных оболочек широко представлено в уже цитированных публикациях. Особо отметим обстоятельный обзор Э.И. Григолюка и Г.М. Куликова [ ПО ] в котором даны классификация используемых гипотез и критический анализ работ именно этого ( общего, по мнению авторов обзора) направления. Григолюка и Г.М. Куликова позволяют не останавливаться на обсуждении конкретных вариантов уравнений слоистых пластин и оболочек, относящихся к рассматриваемому направлению. Большее внимание в настоящей монографии будет уделено лишь одному из таких вариантов, основанному на кинематической модели ломаной линии и получившему ( см. [52, 111, 115] и др.) широкую известность и признание - соответствующая система дифференциальных уравнений статики и устойчивости слоистых оболочек сформулирована в параграфе 3.7. Эта система используется при сравнительном анализе результатов расчета слоистых оболочек с привлечением различных уточненных моделей их деформирования. [11]
В настоящей главе рассмотрен класс упругих ортотропных слоистых цилиндрических оболочек. Линеаризованные уравнения статики таких оболочек получены из общей системы неклассических уравнений (3.5.1) - (3.5.7) и использованы при исследовании осесимметричного деформирования оболочки, нагруженной внутренним давлением. Выполнен параметрический анализ влияния поперечных сдвигов на интегральные ( прогибы, усилия, моменты) и локальные ( нагрузки начального разрушения) характеристики напряженно-деформированного состояния оболочки. Дано решение задачи об устойчивости равновесия цилиндрической многослойной оболочки, нагруженной внешним давлением. Эта задача рассмотрена на основе как уравнений (3.3.4), (3.3.5), так и других ( см. параграф 3.7) вариантов уравнений устойчивости. Выполнен сравнительный анализ результатов расчета, что позволило оценить влияние поперечных сдвиговых деформаций, обжатия нормали, неоднородности докритических усилий на критические параметры устойчивости. [12]
Страницы: 1