Погрешность - второе - вид
Cтраница 1
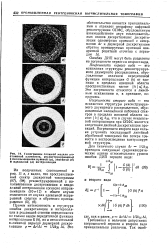 |
Томограммы сложной модели постоянной плотности, реконструированные с использованием нулевой ( а, линейной ( о И идеальной ( в интерполяции. [1] |
Погрешности второго вида - это искажения структуры реконструируемого двумерного распределения, обусловленные наложением побочных спектров в пределах основной области частот k; Нм, что в случае неидеальной интерполяции при ОПФС является следствием двойной дискретизации проекций. [2]
Из (2.24) видно, что погрешность второго вида ег при определенном значении е0 обратно пропорциональна е С уменьшением приращений АФЛ или перемещения Д7 погрешность второго вида возрастает. [4]
С учетом высокой эффективности и простоты метода ОДИП-1 применение метода ОДИН-2 по-видимому целесообразно лишь при наиболее жестких требованиях к величине погрешностей второго вида. В ряде случаев может оказаться эффективным сочетание обоих методов оптимизации. [5]
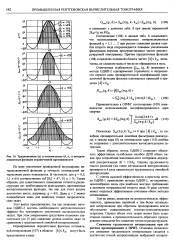 |
Традиционные ( а и оптимальные ( б, в, г интерполяционные функции ограниченной протяженности. [6] |
С учетом высокой эффективности и простоты метода ОДИП-1 применение метода ОДИП-2, по-видимому, целесообразно лишь при наиболее жестких требованиях к величине погрешностей второго вида. В ряде случаев может оказаться эффективным сочетание обоих методов оптимизации. [7]
Из (2.24) видно, что погрешность второго вида ег при определенном значении е0 обратно пропорциональна е С уменьшением приращений АФЛ или перемещения Д7 погрешность второго вида возрастает. [8]
Существо метода ОДИП-2 сводится к выбору минимальной по протяженности и оптимальной по структуре интерполяционной функции gonr ( q, r) с целью добиться ( при ограниченной трудоемкости) необходимого снижения наиболее опасных погрешностей ДИП второго вида. При этом соответствующей модификацией ядра свертки Лопт ( Ц г) в необходимых пределах компенсируется тенденция к росту погрешностей ДИП первого вида. [9]
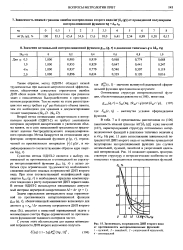 |
Зависимость погрешности ДИП второго вида от протяженности интерполяционных функций. [10] |
Существо метода ОДИП-2 сводится к выбору минимальной по протяженности и оптимальной по структуре интерполяционной функции gonT ( q, r) с целью добиться ( при ограниченной трудоемкости) необходимого снижения наиболее опасных погрешностей ДИП второго вида. При этом соответствующей модификацией ядра свертки hom q, r) в необходимых пределах компенсируется тенденция к росту погрешностей ДИП первого вида. [11]
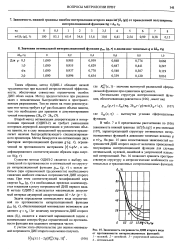 |
Зависимость погрешности ДИП второго вида от протяженности интерполяционных функций. [12] |
Существо метода ОДИП-2 сводится к выбору минимальной по протяженности и оптимальной по структуре интерполяционной функции gorn ( q, r) с целью добиться ( при ограниченной трудоемкости) необходимого снижения наиболее опасных погрешностей ДИП второго вида. При этом соответствующей модификацией ядра свертки АОПТ ( q, г) в необходимых пределах компенсируется тенденция к росту погрешностей ДИП первого вида. [13]
В табл. 7 и 8 представлены рассчитанная по ( 106) зависимость нижней границы inf [ 82 ( q) ] и ряд значений ( 107), характеризующий структуру оптимальных интерполяционных функций в диапазоне типичных величин q и г / гм. На рис. 15 дано сопоставление зависимостей погрешностей ДИП второго вида от величины приведенной полуширины интерполяционной функции для случаев оптимальной, нулевой, линейной и укороченной идеальной интерполяций. [14]
В табл. 7 и 8 представлены рассчитанная по ( 106) зависимость нижней границы inf [ 62 ( q) ] и ряд значений ( 107), характеризующих структуру оптимальных интерполяционных функций в диапазоне. На рис. 15 дано сопоставление зависимостей погрешностей ДИП второго вида от величины приведенной полуширины интерполяционной функции для случая оптимальной, нулевой, линейной и укороченной идеальной интерполяции. [15]
Страницы: 1 2
