Погрешность - вычисление
Cтраница 3
Оценить погрешности вычисления производных в задачах 1 а), б) и 2 а), б) из § 1, считая, что все табличные значения yt даны с верными знаками. [31]
За погрешность вычисления среднего коэффициента песчанистости в формуле (5.37) принимается величина его стандартного отклонения. [32]
Оценки погрешности вычисления этим алгоритмом времени управления и выходной величины в момент t NAt подобны оценкам (25.17) и (25.19) [30], и мы их приводить не будем. [33]
Теория погрешностей вычислений - раздел вычислительной математики, изучающий причины возникновения и способы оценки всевозможных погрешностей решения задач на ЭВМ. [34]
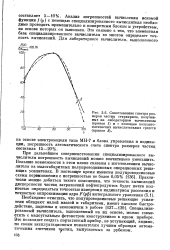 |
Сопоставление спектра размеров частиц стиракрила, полученных на лабораторном вычислителе ( кривая 1 и с помощью полуавтоматических вычислительных средств ( кривая 2. [35] |
Анализ погрешностей вычисления искомой функции / ( р) с помощью специализированного вычислителя необходимо проводить применительно к конкретным блокам и устройствам, на основе которых он выполнен. Это связано с тем, что элементная база специализированного вычислителя во многом определяет точность вычислений. [36]
Чем обуславливаются погрешности вычислений при проведении расчетов на ЭВМ. [37]
При этом погрешность вычислений не выйдет за пределы, обусловленные исходными допущениями. [38]
Проведите исследование погрешности вычисления производных разных порядков с помощью конечно-разностных аппроксимаций. По результатам исследования напишите модуль, содержащий подпрограммы численного дифференцирования с максимально возможной точностью. [39]
При оценке погрешностей вычислений часто пользуются понятиями абсолютной и относительной погрешностей. Эти понятия подобны соответствующим понятиям теории измерений и определяются аналогично. [40]
В пределах погрешности вычислений можно утверждать, что подземные потери газа при эксплуатации подземного хранилища отсутствуют. [41]
В пределах погрешности вычислений можно утверждать, что подземные потери газа при эксплуатации Щелковского подземного хранилища отсутствуют. [42]
Для оценки погрешностей вычислений широко используется экспериментальный ( математический эксперимент) метод оценки погрешности. Он заключается в следующем. [43]
Для оценки погрешности вычислений шаг формулы численного интегрирования увеличивают вдвое, т.е. уменьшают вдвое т, и находят значение интеграла. В этом случае не надо вычислять новые значения функции: так как т входит в знаменатель остаточного члена формулы трапеций в квадрате, то с уменьшением т вдвое остаточный член увеличивается вчетверо. [44]
Для оценки погрешности вычислений и для контроля величины шага применяется правило двойного пересчета. [45]
Страницы: 1 2 3 4