Подпространство - вектор
Cтраница 1
Подпространство векторов, отображающихся в нулевой вектор, называется ядром отображения А. [1]
Его лезвие - это подпространство векторов, у которых первые s компонент равны нулю. [2]
Наиболее интересные элементы Л всегда принадлежат подпространству П гладких векторов или даже еще меньшему подпространству Лш аналитических векторов. [3]
Переходим теперь к следующему подпространству Ог, измерения rj j, причем гг: гг. Из этого подпространства гг векторов уже использованы при предыдущем построении ортов. Используя остальные ( / г 1 - /) векторов совершенно так же, как это мы делали выше, мы построим ( rl l - гг) инвариантных подпространств, в каждом из которых наше линейное преобразование при сделанном выборе ортов будет выглядеть в виде матрицы / г ( 0) порядка ( / - 1) канонической формы. [4]
В [469] процесс дискретного продолжения осуществляется с одновременной редукцией размерности разрешающей системы путем ее отображения по Бубнову на подпространство аппроксимирующих векторов. [5]
Преимуществами блочного наблюдателя на скользящих режимах по сравнению с классическим асимптотическим наблюдателем Калмана [3] являются: 1) выявление наблюдаемого подпространства вектора состояния максимальной размерности; 2) возможность оценить внешние ограниченные возмущения, не повышая порядок наблюдателя; 3) декомпозиция задачи синтеза на независимо решаемые подзадачи меньшей размерности; 4) решение задачи наблюдения за конечное время; 5) обеспечение инвариантности к параметрическим изменениям; 6) облегчение настройки наблюдателя за счет неравенств. [6]
Более того, во всех учебниках линейной алгебры доказывается, что каждое подпространство W и-мерного векторного пространства V может быть задано системой соотношений ( Б) ( быть может, единственным соотношением ( А)), связывающих координаты принадлежащих этому подпространству векторов. [7]
О, )) заключается в том, что если невозмущенная система наблюдаема ( свойства пары [ / 7j ( x, u t), h ( x u t) ] [6]), то построение наблюдателя состояния позволяет оценить все неизмеряемые компоненты вектора состояния. В силу этого, для системы ( 1) ставится задача выявления и оценивания наблюдаемого подпространства вектора состояния максимально возможной размерности и некоторых линейных комбинаций вектора внешних возмущений в рамках блочного метода синтеза. Заметим, что здесь и далее наблюдаемость понимается в локальном смысле. В разделе 3 на основе полученной БНФВ разработан каскадный синтез наблюдателя состояния с разрывными управляющими воздействиями, позволяющий последовательно получить за конечное время оценки неизмеряемых компонент вектора состояния и возмущений. [8]
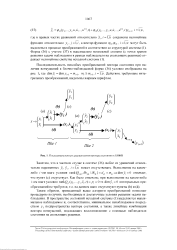 |
Последовательность расщепления вектора состояния к БНФВ. [9] |
Таким образом, приведенный выше алгоритм преобразований позволяет процедурно получить необходимые и достаточные условия решения задачи наблюдения. В пространстве состояний исходной системы ( 1) выделяются максимальное наблюдаемое и, соответственно, минимальное ненаблюдаемое посредством yl подпространства вектора состояния, а также линейные комбинации вектора возмущений, подлежащих восстановлению с помощью наблюдателя состояния на скользящих режимах. [10]
Данная процедура состоит из конечного числа шагов и заключается в расщеплении исходной системы ( 1) на блоки, размерность которых соответствует индексам наблюдаемости системы ( 1) с учетом возмущений. Конструктивность процедуры заключается в том, что структура системы с точки зрения наблюдаемости раскрывается в ходе локальных преобразований, по окончании которых преобразованная система готова к каскадному синтезу. На каждом шаге процедуры выполняются интегральные преобразование, суть которых подробно описана ниже для первого шага. Этот метод, разработанный в [7, 8] на основе использования аппарата дифференциальной геометрии [9] для представления нелинейной системы в регулярной форме относительно управлений, применяется в данном случае для представления блоков наблюдаемой формы нелинейной системы в регулярной форме относительно внешних возмущений. В результате преобразований выделяется наблюдаемое независимо от внешних возмущений подпространство вектора состояния максимальной размерности, а также линейные комбинации компонент вектора возмущений, которые могут быть восстановлены с помощью наблюдателя состояния на скользящих режимах. [11]
Страницы: 1