Подсчет - дебит
Cтраница 2
Следовательно очевидно, что при Fo Fo кр, т.е. когда справедлива простая формула Чекалюка, ею с весьма малой погрешностью можно пользоваться для подсчетов дебита скважины в условиях конечного пласта. [16]
Вообще формула Костикова всюду дает завышенные значения, что при использовании водозаборов для целей водоснабжения может привести к нежелательным осложнениям. Наоборот, подсчет дебита по формулам Дюпюи и Чугаева, а также по сеткам движения приводит к некоторому занижению дебита водозабора, что вполне себя оправдывает, так как создает некоторый резерв при эксплоатации водопровода. Совершенно неприемлемые данные получаются при пользовании формулами Козлова и Лейбензона. [17]
Породы карбонатной и терригенной толщи, даже песчаники, имеют очень малую проницаемость, а именно от десятитысячных до сотых долей дарси. Если использовать даже максимальные значения газопроницаемости пород карбонатной толщи для подсчетов дебита газа, получаются цифры в сотни раз меньшие действительного дебита. [18]
Данный метод называется методом Борисова и позволяет сложный фильтрационный поток в пласте при совместной работе нескольких батарей эксплуатационных и нагнетательных скважин разложить на простейшие потоки - к одиночно работающей скважине и к одиночно работающей батареи. Реализация данного метода достигается введением понятий внутреннего и внешнего фильтрационных сопротивлений, которые придают простейший физический смысл членам уравнений, используемых для подсчетов дебитов и значений потенциальных функций. Для выяснения этих понятий сравним формулы (4.35) или (4.36) с законом Ома IU / R, где I - ток, U - разность потенциалов и R - сопротивление. Из сравнения видно, что фильтрационное сопротивление определяется величиной знаменателя правой части (4.35), который состоит из двух слагаемых. [19]
В формуле (16.36) Qc - это изменяющийся ( уменьшающийся) со временем дебит скважины, пущенной при мгновенном понижении забойного давления с величины PQ до рс, причем давление рс потом удерживается постоянным. Величина ( растущая со временем) приведенного радиуса влияния гир скважины определяется так, чтобы в любой момент дебит скважины можно было представить с помощью формулы (16.36), совпадающей по виду с формулой Дюпюи для подсчета установившегося дебита скважины в условиях жестко водонапорного режима. [20]
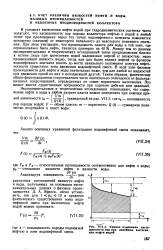
В заключение заметим, что большинство формул этой главы, как уже указывалось, было выведено при приближенном допущении, что точечные источники-стоки помещались в центрах нагнетательных или эксплуатационных скважин. Однако сравнение с более точными формулами показывает, что, например, при Дс 0 001ЯК и d Q. QRK ( рис. 161) ( это сравнительно весьма неблагоприятный случай, ибо в большинстве задач, связанных с технологией нефтедобычи, d и Дс имеют еще меньшие значения по сравнению с RK) ошибка в подсчете дебита по приближенной формуле выражается в тысячных долях процента, т.е. практически не имеет никакого значения. [21]
 |
Кривая изменения насыщенности пор при линейном вытеснении нефти водой. [22] |
В условиях вытеснения нефти водой при гидродинамических расчетах часто полагают, что насыщенность пор породы коллектора нефтью и водой в любой точке при прохождении через эту точку водонефтяного контакта изменяется мгновенно ( скачком) от некоторого начального до некоторого конечного значения. Между тем по данным экспериментальных и теоретических исследований такое предположение близко к истине лишь при вытеснении водой маловязких нефтей ( с вязкостью, мало превышающей вязкость воды), тогда как для более вязких нефтей за фронтом водонефтяного контакта вплоть до места начального положения контура нефтеносности существует зона движения водонефтяной смеси. В этой зоне фазовые проницаемости для нефти и воды значительно ниже, чем для любой из жидкостей при движении одной из них и неподвижной другой. Таким образом, фактические общие фильтрационные сопротивления часто значительно отличаются от фильтрационных сопротивлений, определенных по схеме поршневого вытеснения. Это может внести существенные погрешности при подсчете дебитов или давлений. [23]
Страницы: 1 2