Рассмотренный подход

Cтраница 1

Рассмотренные подходы к изучению школьного образования не являются общепринятыми. Их преимущество в том, что они позволяют объединить существующую информацию демографической статистики, ведомственной статистики школьного образования, данные выборочных социологических опросов школьников в единый мониторинг развития школьного образования. Такой мониторинг может быть осуществлен органами статистики в каждом субъекте Российской Федерации. [1]

Рассмотренный подход, как уже отмечалось, позволяет провести процесс аппроксимации системы наиболее простым и наглядным способом, т.е. является наиболее эффективным с алгоритмической точки зрения. [2]

Рассмотренный подход предполагает, что функция f ( x p t) может быть разложена в ряд Маклорена; если же нелинейная функция не является аналитической, то можно воспользоваться статистической линеаризацией. Алгоритм получения оценок остается прежним. [3]

Рассмотренный подход к определению требований к достаточно точной работе ТА не исключает возможности их работы со значительно большими погрешностями. [4]

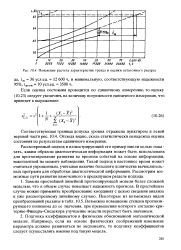Пояснение расчета характеристик тренда и оценки остаточного ресурса. [5]

Рассмотренный подход и иллюстрирующий его пример имели целью показать, каким образом диагностическая информация может быть использована для прогнозирования развития во времени событий на основе информации, накопленной на момент наблюдения. Такой подход в настоящее время может считаться упрощенным, учитывая наличие большого количества вычислительных программ для обработки диагностической информации. Рассмотрим возможные пути развития намеченного в предыдущем разделе подхода. [6]

Рассмотренный подход к фрейм-проблеме основывается на том, что в мире имеется один источник действия ( робот), Этот подход вряд ли может быть применен в общем случае. [7]

Рассмотренный подход к решению задачи идентификации динамических систем на основе нейросетевых модельных структур представляет собой многоэтапную процедуру, на каждой стадии которой решается ряд концептуально значимых подзадач. Последовательное решение именно этих подзадач с использованием рассмотренных рекомендаций обусловливает эффективность метода. Несмотря на мощные обобщающие свойства нейросетевых структур, предложенный подход не является панацеей, так как качество идентификации прежде всего основано на информативности экспериментальных данных. Значительная часть материалов, представленных в данной главе, посвящена именно вопросам эффективного извлечения информации из множества данных, полученных в результате проведения тщательно спланированного эксперимента. [8]

Рассмотренные подходы к определению интенсивности техногенных нагрузок на водные ресурсы по типам источников и видам загрязнения, позволяют оценить общие масштабы ( в пределах административных территорий) загрязнения водных объектов различными загрязнителями, смываемыми поверхностным стоком с площадей определенного функционального назначения. [9]

Рассмотренный подход применим и для ионных частиц. [10]

Значение интервалов восстановления для различных /. ал. [11]

Рассмотренный подход может быть обобщен на любую параметрическую модель старения, при этом основное внимание уделяется методу идентификации модели. [12]

Рассмотренные подходы отражают базовые принципы, которые не могут служить рецептами, достаточными для оценки новизны любого изобретения. Так, существуют особенности при проверке новизны заявок, содержащих альтернативные признаки, частично присущие и прототипу; имеются приемы проверки новизны изобретений, признаки которых представлены интервалами значений, частично совпадающими с интервалами тех же величин прототипа. [13]

Рассмотренный подход выявляет различия между калькуляцией затрат по изделиям на основе сумм покрытия и традиционной калькуляцией полных затрат, составляя которую экономист верил, что с помощью определения себестоимости он может рассчитать сумму затрат, обусловливающую одно изделие на предприятии, и что из этой суммы он может вывести цену предложения. [14]

Рассмотренные подходы обладают одним недостатком. Поперечные сдвиги и, вследствие использования закона Гука, поперечные касательные напряжения распределены равномерно по толщине &-го слоя. В этой главе, следуя работам [2.9, 8.2, 8.3], строится непротиворечивый с точки зрения смешанного вариационного принципа геометрически нелинейный вариант теории многослойных анизотропных оболочек, в котором поперечные компоненты тензора напряжений являются непрерывными функциями поперечной координаты всюду в теле оболочки, в том числе и на поверхностях раздела слоев. При этом на граничных поверхностях они принимают заданные значения. [15]

Страницы: 1 2 3 4