Закон - стокс
Cтраница 3
 |
Автоматический вискозиметр периодического действия. [ IMAGE ] Вискозиметр с коаксиальными цилиндрами. [31] |
Закон Стокса применим для ламинарного движения однородной жидкости относительно строго сферического шарика. [32]
 |
Зависимость степени каустификации от содержания Na2COs в исходном растворе. [33] |
Закон Стокса применим для частиц определенных размеров. Нижний предел ограничен размерами частиц от 0 1 до 0 5 ( J. Верхний предел применимости закона Стокса зависит, кроме того, от плотности частиц, а также от физических свойств жидкой фазы. [34]
Закон Стокса приближенно можно применять для шламов каустификации, если содержание в них дисперсной фазы не превышает 10 % от общего объема суспензии. [35]
Закон Стокса справедлив для Rel, при 1 Re 10 начинают играть более заметную роль инерционные силы и закон Стокса ( пунктирная часть линии 2) не согласуется с экспериментальными данными. При Re 100 система вихрей распространяется вокруг сферы на расстояние одного диаметра. Рейнольдса, влияние инерционных сил нарастает и система вихрей образует след. При Re ж Ю5, которое называется верхним критическим числом Рейнольдса, ламинарный пограничный слой полностью переходит в турбулентный. [36]
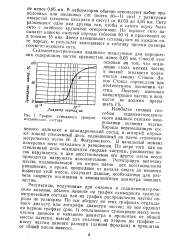 |
График суммарного метрического состава. [37] |
Закон Стокса справедлив при нестесненном движении частиц. [38]
Закон Стокса в первоначальной форме выражает силу сопротивления, которую испытывает шар при медленном движении в жидкости. [39]
Закон Стокса имеет место только для ламинарного движения. [40]
 |
Принципиальная схема авто - [ IMAGE ] Принципиальная схема автоматического капиллярного вискозиметра матического вискозиметра дискретного непрерывного действия действия с падающим шариком. [41] |
Закон Стокса применим при ламинарном течении жидкости относительно шарика. Вискозиметр с падающим шариком весьма чувствителен к загрязнениям жидкости и наличию пузырьков газа в ней, поэтому его можно применять для измерения вязкости только однородных жидкостей. [42]
Закон Стокса - Ломмеля имеет весьма общее значение и строга выполняется для широкого круга веществ. [43]
Закон Стокса часто используют для описания движения частиц молекулярных размеров в жидкостях, хотя для этого нет строгих оснований. Для движения маленьких частиц в газах закон Стокса совершенно несправедлив. Подвижность частиц, размеры которых сравнимы с длиной свободного пробега, хорошо описываются эмпирической формулой Малли-кена. Фукс и И. Б. Стечкина [8] вывели теоретически формулу для подвижности маленьких частиц в газе. [44]
Закон Стокса имеет место толМго для ламинарного движения. [45]
Страницы: 1 2 3 4