Характеристический полином

Cтраница 3

Подобные матрицы имеют одинаковые характеристические полиномы. [31]

Доказать, что характеристический полином оператора на всем пространстве делится на характеристический полином на инвариантном подпространстве. [32]

Плоскость в координатах а и а, на которой показана границ области устойчивости и область допустимых процессов. [33]

Таким образом, характеристический полином эталонного изображения зависит от двух коэффициентов а и а [, которые можно менять из условия обеспечения заданного качества управления. [34]

Это же значение характеристического полинома было вычислено еще в первом издании настоящей книги, вышедшем в 1999 году ( формула ( 99)), и ни у кого сомнений не вызвало. [35]

Для определения корней характеристического полинома приравниваем его к нулю и решаем полученное уравнение. [36]

Итак, для характеристического полинома Михайлова имеем: IM - число левых корней; гм - число правых корней; / м - число нейтральных корней. [37]

Один из корней характеристического полинома объекта ( левый) оставляем на месте. [38]

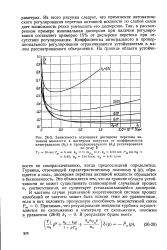Зависимость отношения дисперсии перетока активной мощности к дисперсии нагрузки от коэффициентов интегрального ( йг и пропорционального ( &2 регулирования по углу б. [39]

Гурвица, отвечающий характеристическому полиному г) ( р), обращается в ноль, дисперсия перетока активной мощности обращается в бесконечность. Это объясняется тем, что на границе области устойчивости не может существовать стационарный случайный процесс и, соответственно, не существует устанавливающейся дисперсии. [40]

Этот полином является характеристическим полиномом в D-изоб-ражениях. [41]

Разомкнутая САУ с характеристическим полиномом второго порядка соответствует колебательному звену. Передаточная функция замкнутой САУ также соответствует колебательному звену. По сравнению с разомкнутой системой увеличивается свободный член характеристического полинома. Это изменяет корни характеристического уравнения. [42]

Достаточно показать, что характеристический полином делится на аннулятор любого вектора. [43]

Как отмечалось выше, характеристический полином Q ( A) получается из собственного оператора Q ( p) простой заменой оператора р на комплексную переменную А. Поэтому достаточно найти собственный оператор. [44]

Достаточно показать, что характеристический полином делитси на аннулятор любого вектора. [45]

Страницы: 1 2 3 4