Искомый полином

Cтраница 1

Искомый полином имеет вид Qe ( x) 7 22 2 59 cos - 0 41 cos 2x 0 18 cos 3 - 0 04 cos 4x 0 01 cos их. [1]

Теперь искомый полином Р ( х) может быть написан в виде формулы, дающей интерполяционный полином Лагранжа для абсцисс at, определенных предыдущим выражением. [2]

Величина Кр, соответствующая искомому полиному, находится в промежутке между ними. [3]

В соответствии с двумя рассмотренными случаями искомые полиномы выбираются на основании одного из двух условий. [4]

Теперь находим среднюю точность приближения полученным из опыта полиномом искомого полинома. [5]

Это соотношение можно рассматривать как расчетную формулу для вычисления коэффициентов ak искомого полинома qn ( х), так как числа а известны, а величины Ф ( i) заданы. [6]

Существует традиционный путь решения этой задачи: сначала определить степень п искомого полинома R ( x), а затем в классе функций, разложимых по системе п ортонормальных с весом Р ( х) полиномов, восстановить регрессию. Таким образом, основное содержание проблемы здесь сводится к определению степени полиномиальной регрессии. [7]

Существует традиционный путь решения этой задачи: сначала определить степень п искомого полинома Жх), а затем в классе полиномов степени п восстановить регрессию. Таким образом, основное содержание проблемы здесь сводится к определению степени полиномиальной регрессии. [8]

Матрица А имеет столько столбцов, сколько надо определить коэффициентов, то есть на единицу больше, степени искомого полинома. Матрица У представляет собой матрицу данных частостей. Нормы полиномов Ph, ю () Н не зависят от fi к могут быть вычислены заранее. [9]

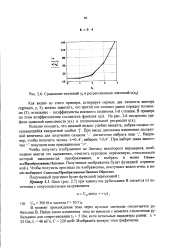Сравнение значений уь и регрессионных значений ufa. [10]

Как видно из этого примера, игнорируя первые два элемента вектора regress ( x, у, 3), можно заметить, что третий его элемент равен порядку полинома ( 3), остальные - коэффициенты искомого полинома 3 - й степени. [11]

Рассмотрим результаты построения эмпирической модели коэффициента конденсатоотдачи с использованием множественной регрессии. Для понижения порядка искомого полинома предварительно выбираются определяющие параметры. [12]

Далее, как об этом уже говорилось, формула (11.19) приводит к квантованию энергии. Здесь же покажем; как вычисляются искомые полиномы. [13]

Короче рассмотреть полином F ( х) xf ( х) - I, где / () - искомый полином. [14]

Теорема 3 допускает следующее применение. Если окажется, что они являются точками перемены знака этой разности и других точек перемены знака на ( - 1, 1) нет, то Рп ( х) и есть искомый полином наилучшего приближения. [15]

Страницы: 1