Политропа
Cтраница 2
Политропу сжатия строят с помощью лучей ОС и OD. Из точки с проводят горизонталь до пересечения с осью ординат; из точки пересечения - линию под углом 45 к вертикали до пересечения с лучом OD, а из этой точки - вторую горизонтальную линию, параллельную оси абсцисс. Затем из точки с проводят вертикальную линию до пересечения с лучом ОС; из точки пересечения - под углом 45 к вертикали линию до пересечения с осью абсцисс, а из этой точки - вторую вертикальную линию, параллельную оси ординат, до пересечения со второй горизонтальной линией. [16]
Политропу расширения строят с помощью лучей ОС и ОЕ, начиная от точки z, аналогично построению политропы сжатия. [17]
Политропу сжатия строят с помощью лучей ОС и OD. Из точки с проводят горизонталь до пересечения с осью ординат; из точки пересечения - линию под углом 45 к вертикали до пересечения с лучом OD, а из этой точки - вторую горизонтальную линию, параллельную оси абсцисс. Затем из точки с проводят вертикальную линию до пересечения с лучом ОС; из точки пересечения - под углом 45 к вертикали линию до пересечения с осью абсцисс, а из этой точки - вторую вертикальную линию, параллельную оси ординат, до пересечения со второй горизонтальной линией. [18]
Политропу расширения строят с помощью лучей ОС и ОЕ, начиная от точки 2, аналогично построению политропы сжатия. [19]
Политропой называется кривая, выражаемая уравнением ух. При и1 кривая превращается в равнобочную гиперболу. При и 1 4 кривая называется адиабатой. Для построения политропы, проходящей через заданную точку М и имеющей показатель п ( рис. III.47, в), проводят прямую О А под произвольным углом а к оси ОХ и прямую О В под углом Р к оси OY. Перпендикуляры к осям, проведенные через эти точки, дают на пересечении точку /, принадлежащую политропе. Так же находят и следующие точки ( 2, 3; 4 и пр. [20]
 |
Построение синусоиды. [21] |
Политропой называется кривая, выражаемая уравнением ухп с, где с - постоянная величина. [22]
Политропой называется кривая, выражаемая уравнением ух с, где с - постоянная величина. При я 1 кривая превращается в равнобочную гиперболу. При л 1 4 кривая называется адиабатой. Для построения политропы, проходящей через заданную точку М и имеющей показатель и ( рис. 111.47, в), проводят прямую О А под произвольным углом а к оси ОХ и прямую О В под углом р к оси OY. Из точек а и b проводят под углом 45 к осям прямые, пересекающие линии О В и ОХ в точках с и d Перпендикуляры к осям, проведенные через эти точки, дают на пересечении точку 1, принадлежащую политропе Так же находят и следующие точки ( 2, 3, 4 и пр. [23]
Политропами описываются не только системы с гладким распределением массы, они могут выступать и в качестве первого приближения систем, содержащих сингулярность или же имеющих очень компактное ядро. Это ядро может представлять собой массивный объект, газовое облако или же плотное звездное скопление, которое может считаться до известной степени изолированным от остальной части системы. Например, в центре скопления галактик может находиться очень массивная галактика; ядро галактики может содержать массивную черную дыру. [24]
Если политропа в указанных координатах - прямая линия, то показатель политропы п на этом участке постоянный п const, если политропа - кривая линия, то показатель политропы п - величина переменная ( фиг. [25]
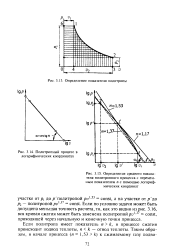 |
Определение показателя политропы.| Политропный процесс в логарифмических координатах.| Определение среднего показа. [26] |
Если политропа имеет показатель п k, в процессе сжатия происходит подвод теплоты, п k - отвод теплоты. [27]
Если эквивалентные политропы не являются адиабатами, а имеют более низкий показатель, то при прочих равных условиях коэффициент Q - будет иметь более низкое значение, чем при эквивалентных адиабатах. [28]
Такая условная политропа называется политропой конечных параметров. [29]
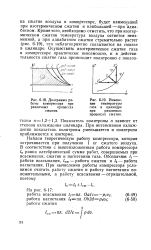 |
Диаграмма работы компрессора при различных процессах сжатия.| Изменение температуры газа в цилиндре при различных процессах сжатия. [30] |
Страницы: 1 2 3 4 5