Положение - линия - регрессия
Cтраница 1
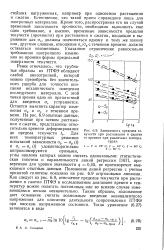 |
Зависимость пределов текучести при растяжении и сжатии от времени при различных температурах. [1] |
Положение линий регрессии с учетом принятой гипотезы показано на рис. 6.9 штриховыми линиями. Как следует из рис. 6.9, отношение пределов текучести при растяжении и сжатии ПТФЭ в исследованном диапазоне времен и температур можно полагать постоянным или во всяком случае изменяющимся весьма незначительно. Таким образом, изложенное дает основание считать возможным введение эквивалентного напряжения для описания длительного сопротивления ПТФЭ при плоском напряженном состоянии. [2]
Спрашивается, как изменится положение линии регрессии, если ее определять не по 16, а по 15 точкам, опустив одно наблюдение в сечении 640 С. [3]
На рис. 5.34 показано положение линии регрессии, а также верхней и нижней границ доверительных интервалов для индивидуальных значений времени до разрыва. [4]
Допустим, что исходные данные были рассеяны в большей степени, но положение линии регрессии не изменилось. [5]
Рассмотренная формула стандартной ошибки предсказываемого среднего значения у при заданном значении xk характеризует ошибку положения линии регрессии. Величина стандартной ошибки т х, как видно из формулы, достигает минимума при хк х, и возрастает по мере того, как удаляется от х - в любом направлении. Иными словами, чем больше разность междухк их, тем больше ошибка трх с которой предсказывается среднее значение у дня заданного значения хк. [6]
Рассмотренная формула стандартной ошибки предсказываемого среднего значения у при заданном значении xk характеризует ошибку положения линии регрессии. Величина стандартной ошибки т х, как видно из формулы, достигает минимума при xk х, и возрастает по мере того, как удаляется от Зс в любом направлении. [7]
Графический анализ разных способов отображения зависимости между исходными значениями показателя и его значениями на этапах полета в двумерной системе координат показал, что для частоты сердечных сокращений наклон линий зависимости, полученных разными способами, отличается от положения линии регрессии незначительно, для частоты дыхания и минутного объема легочной вентиляции эти различия существенны. Линии регрессии вида аХ - f - Ъ наиболее точно описывают полученные экспериментальные данные. [8]
В принципе можно записать выражение для ортогональной регрессии ( к этому вопросу вернемся после рассмотрения коэффициента корреляции), однако ортогональная регрессия, где расстояния от экспериментальных точек до прямой регрессии измеряют по перпендикуляру к этой прямой, находит ограниченное применение, так как положение линии регрессии в системе координат зависит от выбранного по осям масштаба. Так, например, если исследуется зависимость сопротивления проводника от температуры, то получают разные модели ортогональной регрессии при использовании шкал Цельсия или Фаренгейта, что недопустимо. [9]
В принципе можно записать выражение для ортогональной регрессии ( к этому вопросу вернемся после рассмотрения коэффициента корреляции), однако ортогональная регрессия, где расстояния от экспериментальных точек до прямой регрессии измеряют по перпендикуляру к этой прямой, находит ограниченное применение, так как положение линии регрессии в системе координат зависит от выбранного по осям масштаба. Так, например, если исследуется зависимость сопротивления проводника от температуры, то получают разные модели ортогональной регрессии при использований шкал Цельсия или Фаренгейта, что недопустимо. [10]
В принципе можно записать выражение для ортогональной регрессии ( к этому вопросу вернемся после рассмотрения коэффициента корреляции), однако ортогональная регрессия, где расстояния от экспериментальных точек до прямой регрессии измеряют по перпендикуляру к этой прямой, находит ограниченное применение, так как положение линии регрессии в системе координат зависит от выбранного по осям масштаба. Так, например, если исследуется зависимость сопротивления проводника от температуры, то получают разные модели ортогональной регрессии при использовании шкал Цельсия или Фаренгейта, что недопустимо. [11]
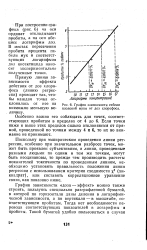 |
График зависимости гибели плодовой мухи от доз хлорофоса. [12] |
Поскольку при эмпирическом проведении линии регрессии, особенно при значительном разбросе точек, может быть проявлен субъективизм, и линии, проведенные разными людьми по одним и тем же точкам, могут быть неодинаковы, то прежде чем производить расчеты показателей токсичности по проведенным линиям, необходимо установить правильность положения линии регрессии с использованием критерия сходимости х2 ( хи-квадрат), или составить корреляционное уравнение связи, как показано ниже. [13]
Страницы: 1