Положение - максимум - спектр
Cтраница 2
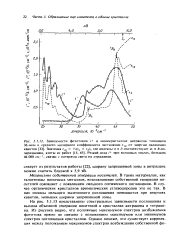
Спектр люминесценции фосфора представляет собой обычно одну или несколько полос, часто довольно широких. Положение максимумов люминесцентных спектров по представлениям зонной теории определяется энергетическим расстоянием между уровнями возбужденного и нормального состояний центра свечения. Если возбужденное состояние центра свечения расположено в разрешенной зоне, то положение максимума в спектре люминесценции будет определяться расстоянием между уровнем центра свечения и серединой соответствующей разрешенной зоны. [16]
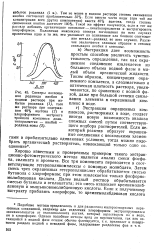 |
Спектры поглощения роданида ниобия в водном растворе при избытке роданида ( 1, того же раствора при содержании 40 % ацетона ( 2 и Хлороформного экстракта. [17] |
Такой же эффект получается, если в тот же paciflop добавить органическое основание - диантипнрилметан и экстрагировать хлороформом. Положение максимума спектра поглощения во всех случаях практически одно и то же; это указывает на одинаковое или близкое соотношение металл-роданид во всех случаях. Различие заключается главным образом в степени связывания ниобия в комплекс. [18]
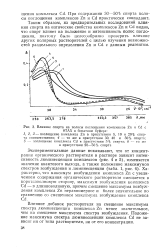 |
Влияние спирта на полосы поглощения комплексов Zn и Cd с. [19] |
Влияние добавок растворителя на смещение максимума спектра люминесценции комплекса Zn менее значительное, чем на смещение максимума спектра возбуждения. Положение максимума спектра люминесценции комплекса Cd не зависит ни от типа растворителя, ни от его концентрации. [20]
 |
Структурные формулы акридиновых. [21] |
Спектры излучения производных акридина являются типичными для красителей - они представляют широкие полосы с одним или несколькими максимумами. В таблице 40 приведены положения максимумов спектров поглощения растворов акридиновых соединений в изоамиловом спирте при 25 С и максимумов спектров излучения веществ в том же растворителе и в кристаллическом состоянии. [22]
Если бы расчеты дава-ли точное значение доплеровского сдвига, частоты, среднее значение частотного сдвига было бы равно нулю. Интересно также то, что положение максимума спектра изменяется от импульса к импульсу. [23]
На рис. 3.1.13 представлены спектральные зависимости поглощения и выхода объемной генерации носителей в кристаллах антрацена и тетраце-на. Из рисунка видно, что положение максимумов спектров возбуждения фототока прямо не связано с положением максимумов или минимумов спектров поглощения кристаллов. [25]
Диссоциация 3-гид-роксила и 6-гидроксила сопровождается сдвигами максимумов спектров поглощения. Отщепление протона последнего имина сопровождается ростом поглощения в дальней ультрафиолетовой части спектра. Положение максимума спектра флуоресценции флуорексона изменяется от 503 лш / с до 511 ммк с диссоциацией 3-гидроксила и от 511 ммк до 520 ммк с диссоциацией 6-гидроксила. [26]
Триптофан, даже если его содержание в белке относительно невысоко, определяет характер спектра флуоресценции последнего. Флуоресценция триптофана возбуждается в области длин волн 170 - 290 нм. Квантовый выход флуоресценции триптофана в водных нейтральных растворах составляет 0 16 - 0 18, а положение максимума спектра флуоресценции приходится на 354 нм. [27]
Приведенной выше программой нельзя воспользоваться для последовательного, поочередного исключения ряда монохроматических помех, потому что спектр каждой монохроматической помехи, если она не целочисленная, занимает все точки отсчета. При помехах одинаковой интенсивности достаточно, чтобы оценки положения частот по положению максимумов получались смещенными. Смещения оценок приводят к неточностям, устранение которых возможно лишь путем подбора правильных значений. Приведенная выше программа в случае ряда помех может быть использована с целью сокращения области подбора правильных значений. Примером такой узкополосной множественной помехи является помеха одной частоты, заданная в виде действительной функции синуса или косинуса, каждая из которых в спектре содержит не одну, а две экспоненты. Эти две экспоненты взаимно влияют на положение максимумов спектра так, что устранить одну составляющую спектра полностью автоматически не удается, действуя по приведенной выше программе. [28]
Анализируемая функция обозначена буквой А. Она представляет собой сумму двух экспонент, одна из которых представляет собою помеху, а вторая - слабый сигнал. Спектр анализируемой функции - G1, а В - его логарифм, нормированный на максимальное значение. На графике, помещенном внизу, показан вид функции В. Дробная частота приводит к тому, что спектр помехи занимает все точки отсчета и с таким уровнем, что сигнала на этом графике не видно совсем. Далее следует программа, автоматически приводящая дробное значение частоты к целому числу путем сдвига всего частотного спектра на величину дробной части частоты помехи. Этому предшествует программа, определяющая дробную часть частоты и состоящая из 4 операций, расположенных в одной строке программы. Строится опорная функция ( АО ], представляющая собой экспоненту целой частоты, которая определяется автоматически по положению максимума спектра А. Программа нахождения этого максимума помещена строчкой выше, она использует встроенную функцию Ф, значения лорой равны нулю для отрицательных значений ее аргумента и единице для нуля и: ех положительных значений. В данном случае аргументом функции Ф является азность между значениями функции и ее максимумом, разность обращается в нуль элько в той точке, в которой ее значение достигает максимума, во всех остальных чках значение аргумента отрицательно. Поэтому функция Ф от аргумента, указан-ого в программе, равна единице в точке максимума функции, а в иных точках она 1вна нулю. В программе функция Ф умножается на значение аргумента, поэтому [ ачение Ф, равное в точке максимума единице, умножается на значение, равное ко-щинате максимума. Это значение является максимальным, так как во всех осталь-ах точках функция Ф равна нулю. Следующим действием определяется максимум 1, в который входит произведение Ф на координату. Этот максимум представляет бою координату максимума спектра ( С / 1 / Программа спектрального анализа cfft в тете Mathcad 6.0 plus устроена так, что наш сигнал попадает во вторую часть спек-а, в которой представлены положительные частоты. Поэтому для сопоставления по-гченного значения координаты максимума спектра с заданной координатой требуется ять разность между полученным значением координаты максимума и длиной всего гссива данных L, что и сделано в программе. [29]
Страницы: 1 2