Помножим

Cтраница 2

Помножим второе уравнение на 3 и сложим с первым. [16]

Помножим каждую строку на I, где / - номер строки. [17]

Помножим это уравнение на Э и проинтегрируем по облает тела. [18]

Помножим это уравнение на ф и проинтегрируем по области тела. [19]

Помножим уравнение ( 1) на / и проинтегрируем по области тела. [20]

Помножим это уравнение на xt и проинтегрируем по области тела. [21]

Помножим обе части равенства на мгновенную силу тока. [22]

Помножим эти матрицы на транспонированную матрицу сопряженных комплексов узловых напряжений. [23]

Помножим эти уравнения на пока произвольные параметры а и сложим их почленно. [24]

Помножим обе части этого уравнения на время t, в пределах которого Р, а значит и п остаются постоянными. Тогда слева получим Р t W - энергию, замеренную счетчиком за время t, а справа п t N - число оборотов диска за это же время. [25]

Помножим кривые / ( / со) при разных п соответственно на годограф, изображенный на фиг. При этом числовые значения векторов перемножаются, а их аргументы складываются. [26]

Помножим эти матрицы на транспонированную матрицу сопря-енных комплексных з зловых напряжений. [27]

Помножим уравнение ( 25) на е - Рт йт и проинтегрируем по т в пределах от О до ос. [28]

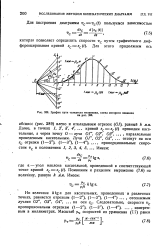График пути толкателя механизма, схема которого показана на 288. [29]

Помножим и разделим выражение (7.6) на величину, равную k мм. [30]

Страницы: 1 2 3 4