Более глубокое понимание
Cтраница 1
Более глубокое понимание того, как работают алгоритмы квантовых вычислений. Это проникновение может осветить путь к новым алгоритмам. [1]
Более глубокое понимание температуры вытекает из анализа того факта, что при равенстве температур не может быть самопроизвольного перехода тепла, и следовательно, тела находятся в тепловом равновесии. Из этого следует, что температура представляет собой самый общий термодинамический параметр, определяющий тепловое состояние тел; в соответствии с приведенной выше классификацией температура относится к числу внутренних интенсивных параметров. [2]
Более глубокое понимание факторов, связывающих парамагнитные свойства РТМ полимеров с их полупроводниковыми характеристиками, было достигнуто изучением взаимодействия кислорода и иода с продуктами РТМ полимеров, полученными в разных условиях. Проявляющиеся при этом взаимодействии особенности обусловлены в случае молекулярного кислорода его парамагнетизмом, а в случае непарамагнитного иода-легкостью, с которой адсорбированные молекулы образуют комплексы с переносом заряда. На полупроводниковые свойства РТМ полимеров влияют как обратимые, так и необратимые процессы, характер которых зависит от термической обработки продуктов. [3]
Более глубокое понимание сложных условий развития показывает, что такое представление о среде является поверхностным. Хотя свет и вода - действительно наиболее доступные в практическом отношении условия среды, в самом зерне, уже с самого момента оплодотворения, существуют и другие факторы, внешние по отношению к хромосомам, несущим гены, которые начинают процесс взаимодействия. [4]
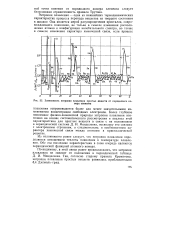 |
Зависимость энтропии плавления простых веществ от порядкового номера элемента. [5] |
Более глубокое понимание физико-химической природы энтропии плавления возможно на основе систематического рассмотрения и анализа этой характеристики для простых веществ в связи с их положением в периодической системе Д. И. Менделеева, поскольку это связано-с электронным строением, а следовательно, и особенностями характера химической связи между атомами в кристаллической решетке. [6]
Более глубокое понимание зависимости средней силы межмолекулярного взаимодействия от температуры может быть достигнуто на основании уравнения состояния Ван-дер - Ваальса. [7]
Более глубокое понимание зависимости средней силы межмолекулярного взаимодействия от температуры может быть достигнуто-на основании уравнения состояния Ван-дер - Ваальса. [8]
Более глубокому пониманию вопроса о емкости способствует разбор качественных задач, в которых рассматривают конденсатор, пластины которого сближают или раздвигают. [9]
Более глубокому пониманию сущности процессов, протекающих в случае деформации при повышенных температурах, способствует параллельное изучение зависимостей напряжение - деформация ( диаграмм деформации) и структурных изменений на разных стадиях деформации для разных температур и скоростей деформации. [10]
Более глубокому пониманию сущности механизмов развития и самоорганизации открытых систем способствуют исследования в области симметрии и асимметрии, которым во второй половине XX столетия естественные науки уделяли значительное внимание. [11]
Более глубокому пониманию сущности собственного капитала способствует его разбивка: а) на капитал, который представляющее отчетность предприятие получает от акционеров, и б) капитал, который оно генерирует своими собственными силами. Вопросы, связанные с собственным капиталом, регулируются в ряде стран юридически. Многие из этих требований влияют на разграничение собственного капитала на средства, которые могут быть распределены, и средства, распределение которых возможно лишь при соблюдении определенных условий. [12]
Это более глубокое понимание пробуждает такую позабытую человеческую способность, как интуиция. [13]
Гораздо более глубокое понимание природы интерполяционных задач было получено в связи с другой областью математики, развитой в течение XIX века, но полностью понятой во всех своих следствиях только в более позднее время. Остроумная геометрическая интерпретация метода наименьших квадратов открыла новое, исключительно благодарное поле для исследований. В этой геометрической картине понятие функции переходит в понятие вектора, принадлежащего пространству бесконечно большого числа измерений. [14]
Страницы: 1 2 3 4