Понятие - среднее значение
Cтраница 1
Понятие среднего значения здесь требует пояснения. [1]
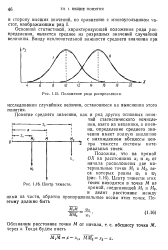 |
Центр тяжести. точек находится в точке М на. [2] |
Понятие среднего значения, как и ряд других основных понятий статистического исчисления, взято из механики, а именно, определение среднего значения имеет полную аналогию с нахождением абсциссы центра тяжести системы материальных точек. [3]
Понятие среднего значения функции очень употребительно в технике. [4]
О понятии среднего значения ( итал. [5]
Равенство (11.29) непосредственно вытекает из математического определения понятия среднего значения переменной величины. [6]
При изучении стационарных случайных процессов в системах управления используют два понятия средних значений: по множеству и по времени. [7]
Кроме действующего значения тока и напряжения, иногда пользуются еще понятием среднего значения тока и напряжения. [8]
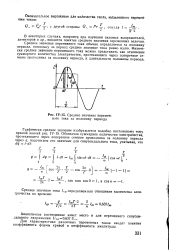 |
Среднее значение переменного тока за половину периода. [9] |
В некоторых случаях, например при изучении силовых выпрямителей, детекторов и др., вводится понятие среднего значения переменных величин. [10]
Для величины же, например, In ( е / е) относительная флуктуация экспоненциально возрастает с увеличением области усреднения, тем самым лишая устойчивого смысла понятие средних значений. [11]
Но помимо математической - есть разница психологическая. Для кого-то понятие среднего значения может быть предпочтительнее понятия вероятности. [12]
Анализ линейных систем управления излагается обобщенное описание задач управления, затем дается последовательный анализ различных аспектов качества систем управления. Одномерные и многомерные системы управления исследуются на основе единого подхода с использованием понятий средних значений квадрата ошибки слежения и квадрата входной переменной. Часть главы посвящена описанию векторных стохастических процессов, при этом особое значение придается представлению стохастических процессов как выходных переменных линейных дифференциальных систем, возбуждаемых белым шумом. [13]
Этот результат часто получает ошибочное толкование, описанное в примере 2 предыдущего параграфа, из-за смешения понятий среднего значения и вероятности. Кардано также смешивал понятия математического ожидания и вероятности, что привело к забвению его исследований по теории вероятностей вплоть до 1953 г., когда О. [14]
Страницы: 1