Понятие - конус
Cтраница 1
Понятие конуса введено в § 12 гл. Нужно иметь в виду, что типичным сечением здесь является гиперболоид. Конусы появляются лишь в отдельных гиперплоскостях ( Xi а, jc2j os); их можно рассматривать как вырожденные гиперболоиды. [1]
В этой главе вводится понятие конуса в банаховом про-рранстве. При помощи конуса в пространстве определяется оотношение полуупорядоченности. [2]
В следующем параграфе мы снова коснемся введенных выше понятий конуса и надстройки, распространив эти понятия па отображения, причем окажется, что эти операции порождают так называемый коварпаптиып функтор в категории топологических пространств. [3]
Силы и моменты сил трения в поступательных кинематических парах обычно рассчитывают с использованием понятия конуса трения. [4]
Второй этап данного алгоритма [213] отличается от [238] более общей постановкой, основанной на использовании понятия конуса доминирования. [5]
Понятие Г - системы на компакте, состоящем из конечного числа точек, оказывается связанным с понятием многогранных конусов в Rn ( конических оболочек конечной системы векторов) с максимальным числом граней при данном числе ребер. [6]
Второй этап данного алгоритма ( см. [48]) отличается от приведенного в работе [45] более общей постановкой, основанной на использовании понятия конуса доминирования. В случае В Е оптимизация таблицы испытаний приведет к построению дискретной аппроксимации всего множества Парето. [7]
За недостатком места мы опустим здесь многие другие результаты по геометрии конусов, полученные М. Г. Крейном и его сотрудниками ( Ю. И. Гросбергом, В. Л. Шмульяном и др.), и перейдем к изложению особого круга исследований в теории операторов, для которого понятие конуса играет определяющую роль. [8]
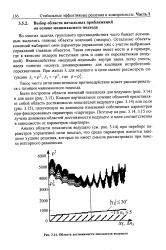 |
Область достижимости показателя ведущего. [9] |
Остальные объекты коалиций выбирают свои параметры управления уже с учетом выбранных управлений главным объектом. Взаимодействие ведущий-ведомый внутри звена легко учесть, введя понятие конуса доминирования для коалиции истребителей-перехватчиков. [10]
Как было отмечено выше, неравенства в теореме 1.5.4 покомпонентные. Вместо того, чтобы рассматривать эти неравенства между векторами, используем понятие конуса, чтобы ввести частичное упорядочение на R и в этих рамках доказать теорему 1.5.4. Естественно, что такой подход является более общим и используется для конусозначных функций. Поэтому даем развитие теории дифференциальных неравенств и доказываем результат, соответствующий теореме 1.5.4, в произвольных конусах. [11]
Страницы: 1