Понятие - нечеткое множество
Cтраница 1
Понятие нечеткого множества является одним из возможных описаний неопределенности результатов измерения. В этом смысле нечеткие множества являются весьма полезным аппаратом для формализации априорной информации и дальнейшего ее использования при обработке данных. В работе [19] рассматривается формализация априорной информации, формируемой экспертом на основе его профессионального опыта, в том числе в результате анализа физической природы объекта измерения, методов измерений, взаимодействия средства измерений с объектом, а также на основе изучения поведения аналогичных объектов и анализа их сходства с данным объектом. [1]
В основе этой теории лежит понятие нечеткого множества, которое является математической формализацией нечеткой информации, используемой при анализе, моделировании и управлении сложными системам ПО. [2]
В основе данной теории лежат понятия нечеткого множества и функции принадлежности, определение которых приводятся ниже. [3]
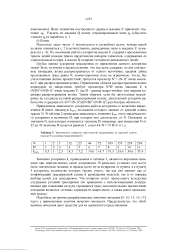 |
Зависимость скорости двухэтапной трассировки от средней длины трассы N и размера макроячейки D. [4] |
Подобные алгоритмы разрабатывались многими авторами [9, 10, 15, 16, 17], часто с применением понятия нечетких множеств. Представляется, что обобщенные описания дают средства для их адекватного представления. [5]
Отметим, что проведенные рассмотрения показывают возможные направления дальнейшего обобщения понятия нечеткого множества, которые могут оказаться полезными в некоторых задачах. [6]
Для формализованного представления задачи поиска аналогов при допущении, что требования на показатели объекта могут выполняться нестрого, целесообразно воспользоваться понятиями нечетких множеств и базирующихся на них методах нечеткого математического программирования. Тогда решаемая задача принятия проектных решений может быть представлена следующим образом. [7]
В реальных ситуациях, связанных с мобильным изменением условий функционирования ХТС, установление таких четких оценок и отношений чаще всего основано на усреднении некоторым образом экспертных оценок. Эти оценки, являясь неточными, отражают лишь определенную долю истины или степени нечеткости утверждений о сходстве объектов относительно каждого признака и их совокупности в целом. В этом смысле более правильными являются методы классификации, основанные на понятиях нечетких множеств и отношений. Обратим внимание на основные методы оценки близости исследуемых объектов. [8]
В этой главе различные понятия и конструкции теории множеств переносятся в теорию категорий. Одновременно определяется специальный класс категорий - топосы, объединяющий различные категории, близкие категории множеств. Объекты топо-сов - это множества, которые, вообще говоря, не обязательно характеризуются своими элементами. В частности, понятие нечеткого множества дается с позиций теории категорий. Все это позволяет рассматривать модели баз данных в условиях неполной или нечеткой информации ( см. гл. [9]
Формально никаких ограничений на функтор h и категорию К можно не накладывать, однако понятно, что переход от алгоритмов к категориям может быть эффективным только в тех случаях, когда функтор и категория обладают хорошими теоретико-категорными свойствами. Мы покажем, что, наложив на К сравнительно слабые ограничения, приходим к классу категорий, по своим свойствам близким к категориям гильбертовых пространств. Именно среди них содержится категория, которую можно рассматривать как теоретико-категорную формализацию понятий нечетких множеств, отношений и функций. Наличие такой формализации, помимо всего прочего, позволяет исследовать нечеткие объекты и построенные на их основе модели с помощью аппарата теории категорий и строить другие, возможно, более точные модели. В частности, используя известные понятия алгебраических объектов и автоматов в категориях ( см. [10]), приходим, соответственно, к нечетким алгебраическим объектам и нечетким автоматам, в которых не только множества состояний являются нечеткими множествами, но и операции - нечеткими функциями. [10]
За последние десятилетия значительное развитие получило нечеткое программирование, которое выделяет естественную множественность целей и значений, неточно определенных подцелей и ограничений. При этом на первые позиции выходят понятия оптимальности в терминах поведения, подчеркивается первостепенное значение знаний, обучения. Широко используется понятие гибкого программирования с его вниманием на начальном этапе анализа не к целям, а к ограничениям. Ограничения возникают в процессе оценки, а Не порождают последний. При этом способы математического описания и анализа разнообразных задач принятия решений на основе нового подхода, опирающегося на введенное Л.А. Заде понятие нечеткого множества [ 18 ], используется для формализации исходной информации об исследуемости реальной ситуации или процесса принятия решений, которые носят субъективный и поэтому нечеткий характер. Именно нечеткий подход и гибкое программирование на его базе позволяют помочь лицу, принимающему решение ( ЛПР), прежде всего, освобождая его от формулировки явных ограничений. При этом теория нечетких множеств тесно связана с нестационарными системами и позволяет нестационарную систему описать как стационарную, если ввести нечеткие параметры, которые отражают способность поглощать неожиданности, встречающиеся в динамических структурах типа систем С участием человека. [11]
Страницы: 1