Понятие - характеристическая функция
Cтраница 1
Понятие характеристической функции, как показано ниже, весьма полезно при решении целого ряда теоретических и практических задач теории вероятностей. [1]
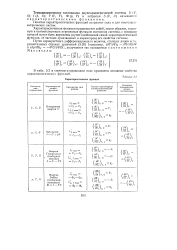 |
Характеристические функции. [2] |
Понятие характеристических функций сохраняет силу и для многопараметрических систем. [3]
Понятие характеристических функций в термодинамику было впервые введено Массье в 1869 г. в работе О характеристических функциях жидкостей. Гиббс дал этим функциям несколько иное определение и последовательно применил их к решению ряда вопросов химической термодинамики. [4]
Обобщением понятия характеристической функции на стохастические процессы является характеристический функционал. В другой связи эта идея была использована в § 2.3.) Пусть Y ( t) - заданный случайный процесс. [5]
Рассмотрим обобщение понятия характеристической функции на основе Нэш-равновесия. [6]
ХАРАКТЕРИСТИЧЕСКИЙ ФУНКЦИОНАЛ - аналог понятия характеристической функции, используемый в бесконечномерном случае. [7]
Основным понятием кооперативной теории является понятие характеристической функции, определяемой на множестве всех коалиций. Система соотношений ( 25: 3: а), ( 25: 3: Ь) и ( 25: 3: с), выражающая основные свойства характеристических функций, по существу является системой аксиом, описывающих естественные свойства тех возможностей, которыми каждая коалиция располагает в наименее благоприятных условиях, именно когда все игроки, не входящие в коалицию, совместно выступают против нее. [8]
Хотя понятие дележа логически и связано с понятием характеристической функции, но в принципе является внешним по отношению к нему. Поэтому уточнение формальной связи между этими понятиями оказывается достаточно плодотворным. Основой этой связи может служить соотношение между выигрышами ( полезностями), получаемыми коалицией на основании характеристической функции, с одной стороны, и на основании того или иного конкретного дележа - с другой. [9]
В связи с теоремой 13 заметим, что понятие характеристической функции для меры на ( Еш, е & ( Еш)) допускает естественное обобщение на более общие пространства. [10]
Отображение ф называется характеристической функцией се-мейства / т - Понятие характеристических функций было рассмотрено Марчевским [2, 10] в случае, когда Т есть множество положительных целых чисел. Метод характеристических функций Марчев-ского несколько раз использован в этой книге. [11]
Понятие предикат играет в теории отношений такую же роль как понятие характеристической функции в теории множеств. Отметим, что унарный нечеткий предикат представляет собой не что иное, как нечеткое множество, выражение (4.3) для нечеткого отношения есть также определение п-арного нечеткого предиката, а запись (4.6) задает бинарный нечеткий предикат. [12]
Мы пришли к формулировке теории общих игр п лиц и установили, что понятие характеристической функции является столь же существенным в теории общих игр п лиц, как и в рассмотренной ранее теории игр с нулевой суммой. Следовательно, имеет смысл проанализировать это понятие еще раз, приведя его математическое определение в явном виде и сопроводив его некоторыми замечаниями интерпретационного характера. [13]
Понятие многочлена, идемпотентного по модулю ( хп - 1) в АТ [ л: ], тесно связано с понятием характеристической функции. [14]
В аппаратах с интенсивным перемешиванием суспензии в рабочем объеме концентрация С / одинакова для всех частиц материала, что дает возможность путем усреднения по всем порам и по всем частицам ввести понятие характеристической функции ft ( у) для массы полидисперсных частиц; при этом частицы могут обладать анизотропными свойствами и иметь произвольную неправильную форму. Функция ft ( у) в общем случае интегрально учитывает все особенности реального материала, а также и величину внешнего сопротивления массоотдачи от наружной поверхности частиц. Как и кинетическая функция в процессе растворения, характеристическая функция здесь наиболее полезна в тех случаях, когда модельные представления о процессе оказываются неудовлетворительными. [15]
Страницы: 1 2