Порядок - полином
Cтраница 1
Порядок полинома соответствует тому порядку разностей, ряд которых образует величины, незначимо отличающиеся друг от друга. [1]
Порядок полинома в знаменателе должен быть равен или превышать порядок полинома в числителе. [2]
Предварительно порядок полинома следует определять методом разностей. [3]
КЗ задают порядок полинома или наибольший номер гармоники и могут быть назначены произвольно. [4]
Число и порядок полиномов Лагранжа определяются количеством узлов конечного элемента. [5]
Дальнейшее увеличение порядка полинома приведет к незначительным эффектам, поэтому на практике целесообразно использовать полином не выше второго порядка. [6]
Обоснованный выбор порядка полинома для метода наименьших квадратов обычно реализуется с помощью статистических тестов, которые уместно использовать в том случае, когда функция р сама является степенным полиномом конечного порядка. [7]
Важно правильно определить порядок полинома и число точек N, по которым вычисляют параметры полинома. Обычно используют сглаживание по пяти и десяти точкам при помощи кривых второго и третьего порядка. [8]
Согласно теории полиномов порядок полинома на единицу меньше числа уровней варьирования факторов. [9]
Следовательно, изменение порядка полинома или опускание в нем хотя бы части членов приводит к изменению численного значения всех остальных коэффициентов регрессии. Такая неопределенность в оценке коэффициентов регрессии крайне затрудняет их физическую интерпретацию. В этом случае уравнение регрессии приходится рассматривать как интерполяционную формулу, пригодную лишь для оценки некоторого промежуточного значения по результатам остальных ( N) значений Уъ У2 Уы - При таком использовании уравнения регрессии перераспределение численных значений для коэффициентов регрессии, связанное с изменением порядка приближения, не будет вызывать каких-либо недоумений. [10]
Следовательно, изменение порядка полинома или опускание в нем хотя бы части членов приводит к изменению численного значения всех остальных коэффициентов регрессии. Такая неопределенность в оценке коэффициентов регрессии крайне затрудняет их физическую интерпретацию. В этом случае уравнение регрессии приходится рассматривать как интерполяционную формулу, пригодную лишь для оценки некоторого промежуточного значения по результатам остальных ( N) значений Уъ У2 Уы - При таком использовании уравнения регрессии перераспределение численных значений для коэффициентов регрессии, связанное с изменением порядка приближения, не будет вызывать каких-либо недоумений. [11]
Так как пъ - порядок полинома, то полученное значение округляется до ближайшего большего целого числа. [12]
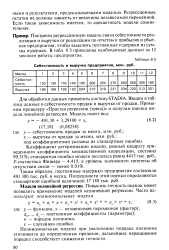 |
Себестоимость и выручка предприятия, млн. руб. [13] |
Полиномиальные модели при увеличении порядка полинома уточняются до определенных пределов, дальнейшее наращивание порядка способствует снижению точности. [14]
Поскольку применение разностного оператора понижает порядок полинома на единицу, получаем, что 8 является полиномом третьего порядка. [15]
Страницы: 1 2 3 4