Потенциал - притяжение
Cтраница 3
Наличие качественного совпадения в данном случае становится тем более замечательным, что при положении равновесия равнодействующий потенциал притяжения составляет лишь малую часть величины потенциала притяжения при пренебрежении межядерным отталкиванием. [31]
В уравнении ( 18) первая составляющая относится к потенциалу отталкивания, а вторая - к потенциалу притяжения. Это уравнение справедливо для инертных газов и простых жидкостей. [32]
Для оценки энергии связи, как это видно из формулы (2.4), необходимо знать хотя бы в общем виде зависимости потенциалов притяжения f / np и отталкивания / 7ОТ от расстояния г между взаимодействующими атомами. Конкретный вид этих зависимостей определяется природой взаимодействующих атомов. [33]
Рассмотрим теперь систему, характеризуемую взаимодействиями того же вида, как и (9.3.2), но наложим дополнительные ограничения иа вид потенциала притяжения Vij. Грубо говоря, рассмотрим предел, в котором глубина потенциала стремится к нулю, но в то же время его радиус действия стремится к бесконечности. В очень важной работе ( 1963 г.) Кац, Уленбек и Хем-мер показали, что для одномерной системы этого типа ( в которой предполагается, однако, экспоненциальная форма потенциала Vij) можно подробно вычислить статистическую сумму. Следовательно, в этой модели имеет место истинный фазовый переход первого рода. Такой результат кажется несколько неожиданным, поскольку давно известно, что одномерные системы не испытывают фазовых переходов, если взаимодействия имеют конечный радиус. Позднее Ван Кампен показал, что поведение типа предсказываемого уравнением Ван-дер - Ваальса - Максвелла можно получить в более общих случаях. Наконец, Лебовитц и Пенроуа в 1966 г. еще более обобщили класс потенциалов и строго показали, что теория фазовых переходов Ван-дер - Ваальса - Максвелла может быть непосредственно получена из выражения для классической статистической суммы; вместе с Либом они обобщили результат на квантовые системы. [34]
Если взаимодействие описывается потенциалом, то в yt дает вклад асимптотика потенциала на больших расстояниях, тогда как df насыщается потенциалом притяжения на малых расстояниях. [35]
Молекулярные орбитали, как правило, представляют собой более сложные математические функции, чем атомные орбитали, так как для них потенциал притяжения определяется не одним, а несколькими ядрами. Кроме того, для них в отличие от атомов при определении отталкивательной части потенциала обычно не проводят какого-либо сферического усреднения электронной плотности. Таким образом, эффективный потенциал для атомной орбитали является сферически-симметричным, а для молекулярной нет. [36]
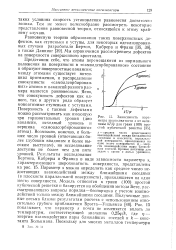 |
Зависимость параметра шероховатости s от величины kT / tp для грани ( 100 простой кубической решетки. [37] |
Представим себе, что атомы перемещаются из нормального положения на поверхности в самоадсорбированное состояние и образуют поверхностные вакансии; между атомами существует потенциал притяжения, и распределение совокупности самоадсорбированных атомов и вакансий разного размера является равновесным. Ясно, что совокупность дефектов как одного, так и другого рода образует моноатомные ступеньки с уступами. [38]
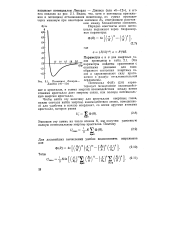 |
Потенциал Ленарда - Джонса ( 6 - 12. [39] |
Ленарда - Джонса ( или 6 - 12), и era вид показан на рис. 2.1. Видно, что, хотя и потенциал притяжения и потенциал отталкивания монотонны, их сумма проходит через минимум при некотором значении Ro, отвечающем расстоянию между ближайшими соседями. [40]
Наличие качественного совпадения в данном случае становится тем более замечательным, что при положении равновесия равнодействующий потенциал притяжения составляет лишь малую часть величины потенциала притяжения при пренебрежении межядерным отталкиванием. [41]
В результате возникает потенциал отталкивания, зависимость которого от межатомного расстояния должна быть такой, чтобы он превалировал на малых расстояниях и был меньше потенциала притяжения на больших расстояниях. Обычно его записывают либо как 5 / R12, либо Яехр ( - / р), где В, К и р - некоторые константы. [42]
При т1 потенциал (2.9) соответствует обычному кулонов-скому взаимодействию между противоположно заряженными ионами, а при т 6, как мы увидим ниже, - потенциалу притяжения при взаимодействии между атомами инертных газов. [43]
В случае молекулы водорода мы имеем дело с орбитальным ] состояниями, принадлежащими различным атомам, так что здеа к потенциалу взаимного отталкивания электронов добавляется потенциал притяжения второго ядра. Тогда вычисления по теории возмущений формально аналогичны расчетам для атома гелия с тем лишь отличием, что к истинному обменному интегралу / 0 добавляется член, который представляет собой поправку к энергии, возникающую за счет силы притяжения, действующей на электрон со стороны второго ядра. Этот отрицательный член может ( при малом расстоянии между ядрами) превышать энергию истинного обменного взаимодействия, так что эффективный обменный интеграл в таком случае может оказаться отрицательным. [44]
 |
Матричные сдвиги полос для различных колебаний молекул. Заштрихована область типичных значений матричных сдвигов. [45] |
Страницы: 1 2 3 4