Потенциал - пространство
Cтраница 2
Этого можно достигнуть, задавая зонду потенциал, точно равный потенциалу пространства в месте установки зонда. [16]
 |
Траектории движения электронов в индикаторе типабЕбС.| Схема включения электронного индикатора.| Устройство индикатора типа 6Е1П. [17] |
При небольшом отрицательном напряжении на управляющей сетке напряжение управляющего электрода ниже потенциала пространства, электроны отталкиваются от него и на экране образуются два затемненных сектора. [18]
При измерениях двойным зондом на него следует подавать потенциал, близкий к потенциалу пространства, для уменьшения влияния на исследуемый разряд. Точного соответствия потенциала зонда потенциалу пространства, как это необходимо для одиночного зонда, здесь не требуется. [19]
При измерениях от специального источника на сетку должно подаваться переменное напряжение, близкое к потенциалу пространства в исследуемой точке, а на зонд - постоянное относительно сетки напряжение. [20]
Основное изменение должно состоять в том, что на зонд следует задавать переменный во времени потенциал, близкий к потенциалу пространства в месте расположения зонда. Естественно, что измерения при этом следует вести при помощи осциллографа. [21]
Поскольку в это уравнение не входит радиус кривизны двойного слоя, то оно справедливо для любой электрической линзы с потенциалом предметного пространства U и с потенциалом пространства изображений V. Справедливость уравнения ( 89) ( также как и уравнений ( 84) м ( 80)) в общем случае следует из того, что электрические линзы с любым распределением потенциала можно рассматривать как последовательное соединение множества двойных слоев. По аналогии и в этом случае должны иметь место те же самые соотношения, что и для отдельного двойного слоя. [22]
Пятая глава посвящена основным эффектам пространственного заряда в коллективах взаимодействующих частиц: закону трех вторых, расплыванию свободных потоков, изменению потенциала пространства, образованию виртуальных катодов. Рассмотрено формирование интенсивных потоков MarHHf ным полем с полностью или частично экранированным катодом. Обсуждается проблема согласования потока, имеющего конечные ток и эмиттанс с периодическим квадрупольным каналом. [23]
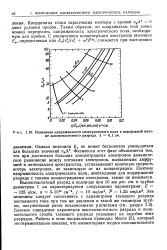 |
Изменение напряженности электрического поля в водородной плазме высокочастотного разряда. Л 0 1. [24] |
Физически этот факт объясняется тем, что при достаточно больших концентрациях электронов динамическое равновесие межцу потоками электронов, вызванными диффузией и потенциалом пространства, устанавливает конечную скорость потерь электронов, не зависящую от их концентрации. Поэтому напряженность электрического поля, необходимая для поддержания разряда с такими концентрациями электронов, также не изменится. Близкое совпадение параметров высокочастотного разряда и положительного столба тлеющего разряда указывает на подобие этих разрядов. [25]
Действительно, на основании ряда зондовых измерений можно было предположить, что перед катодом накапливается положительный пространственный заряд настолько значительный, что потенциал пространства в этой области оказывается много выше напряжения разряда и во всяком случае выше, чем самый низкий потенциал возбуждения. Вопрос о том, как возникает этот пространственный заряд и каким образом электроны приобретают энергии, достаточные для преодоления тормозящего действия отрицательного поля между пространственным зарядом и анодом, до сих пор остается открытым. Ток на анод в этом случае может протекать через эту область только при условии, если диффузионная скорость дрейфа будет превышать скорость дрейфа в отрицательном поле: последнее возможно лишь при значительных градиентах концентрации н высоких температурах электронов. Экспериментальные факты, выдвигаемые в подтверждение такой схемы, неубедительны. Например, предполагается, что существует ограниченная область высокого положительного потенциала, в которой наблюдается интенсивное свечение ( огненный шар) и которая не пропускает электронов, так что ток, текущий на анод, должен был бы огибать область этого свечения. [26]
Поскольку в это уравнение не входит радиус кривизны двойного слоя, то оно справедливо для любой электрической линзы с потенциалом предметного пространства U и с потенциалом пространства изображений V. Справедливость уравнения ( 89) ( также как и уравнений ( 84) м ( 80)) в общем случае следует из того, что электрические линзы с любым распределением потенциала можно рассматривать как последовательное соединение множества двойных слоев. По аналогии и в этом случае должны иметь место те же самые соотношения, что и для отдельного двойного слоя. [27]
Влияние зондов на главный разряд снимается благодаря тому, что переменное напряжение, задаваемое на зонды от специального источника, во все моменты времени близко по величине к потенциалу пространства, существующему в месте установки зондов до их внесения в исследуемое поле. Необходимые при измерениях амплитуда, фаза и форма этого напряжения ( компенсация пространственного потенциала) устанавливались на основании критерия компенсации, в качестве которого при применении дифференциального зонда принималось совладение вольт-амперных характеристик исследуемого разряда до и после внесения зонда. Пространственный потенциал, как и в случае зонда с сеткой, компенсировался путем регулирования амплитуды и фазы источников компенсирующего напряжения основной и тройной частот. [28]
При рассмотрении движения электронов в электростатических линзах следует учитывать то, что в отличие от кванта света в оптических средах электрон в линзе изменяет свою энергию в соответствии с изменением потенциала пространства. Очевидно также, что характер изменения траектории электрона будет зависеть от скорости, с которой он попадает в поле линзы. Более быстрые электроны отклоняются в поле линз слабей, чем более медленные. Следовательно, параметры линз связаны со скоростями электронов. Обычно все потенциалы электродов электронно-оптических систем отсчитываются от катода, потенциал которого принимается за нуль. В этом случае, если пренебречь величиной начальных скоростей электронов, выходящих из катода ( обычно термоэлектронного), параметры линз определяются геометрией н потенциалами электродов. [29]
Количественная связь между анодным током и анодным напряжением в режиме объемного заряда ( пока не все электроны, поки-дающие катод, достигают анода) может быть найдена из решения уравнения Пуассона, связывающего потенциал пространства с плотностью р объемного заряда. [30]
Страницы: 1 2 3 4