Предыдущее замечание
Cтраница 3
Учтя все предыдущие замечания, мы теперь можем написать полную программу, использующую описанные нами процедуры. [31]
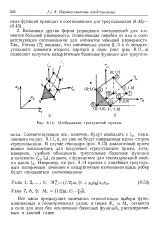 |
Отображение трехгранной призмы. [32] |
Все наши предыдущие замечания относительно выбора функциональных и геометрических узлов, а также Na и Мл остаются в силе для всех без исключения базисных функций, рассматриваемых в данной главе. [33]
На основании предыдущих замечаний приходим к выводу, что точки неизменной плоскости Лапласа соответствуют наибольшим секторным скоростям. [34]
Из двух предыдущих замечаний вытекает, как мы знаем, справедливость той теоремы, которую мы имели в виду доказать. [35]
С учетом предыдущих замечаний неудивительно, что конечность ветвления находит столь явные и четко очерченные области применения в тех случаях, когда фрактальная геометрия оказывается призвана подробно определить, в какой пропорции плоская фрактальная кривая сочетает в себе два своих стандартных предела: прямую и плоскость. Обобщая, можно сказать, что знать фрактальную размерность кривой отнюдь не достаточно. [36]
В силу предыдущих замечаний можно всюду считать, что g - Q и что, следовательно, мера Я положительна. [37]
В силу предыдущих замечаний остается только показать, что если Е и удовлетворяют условиям предложения, то отображение и, определяемое равенством (9.5.12), непрерывно. [38]
В свете предыдущих замечаний довольно удивительно, что формулу (9.11.9), куда не входят XQ и yQ, можно сохранить. Этот факт опирается на одно замечание, которое представляет собой частный случай следующей леммы. [39]
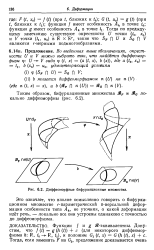 |
Диффеоморфные бифуркационные множества. [40] |
Тогда по предыдущему замечанию существуют окрестности U точки ( / 0, х0) и V точки ( tlt ы0) в R X Rr. SF f ] U и S0 fl V являются r - мерными подмногообразиями. [41]
Ибо, согласно предыдущему замечанию, интеграл от разности f ( х) - g ( х) имеет неотрицательное значение, а по правилу интегрирования суммы ( стр. [42]
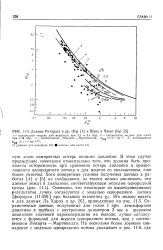 |
Данные Ричардса и др. ( Н2 и Шена и Чжао ( N2. [43] |
В этом случае предыдущие замечания относительно того, что должна быть проявлена осторожность при сравнении потерь давления в предположении однородности потока и для модели со скольжением, еще более уместны. Очевидно, что некоторые из вышеприведенных результатов лучше согла ауются с моделью однородного потока [ формула ( Н-29) ] при больших значениях itt - Это можно в идеть и для данных Л а Харпа и др. [6], приведенных на рис. 11.5. Ограниченные: даиные, полученные для гелия I при атмосферном давлении в трубках с внутренним диаметром 3 мм в широком диапазоне значений пароеодержания на выходе, лучше согласуются с формулой для модели однородного потока, чем с соотношением Локарта - - Мартинелли. [44]
В этом смысле предыдущее замечание можно сформулировать так: равновесие, имьюшее место при действии консервативных сил в конфигурации действительного максимума для потенциала, обладает также и вековой устойчивостью. [45]
Страницы: 1 2 3 4