Замораживание - орбитальный момент
Cтраница 1
Замораживание орбитального момента упрощенно и наглядно можно представить следующим образом. [1]
В зарубежной литературе принят термин замораживание орбитального момента. [2]
Отсутствие для этого иона сколь-нибудь заметного замораживания орбитального момента динамическим эффектом Яна - Теллера обсуждается в § 12 гл. [3]
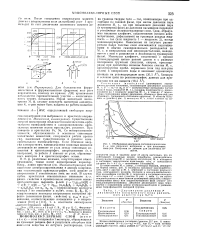 |
Обобщенная диаграмма состояния монослоев F-а для широкого интервала а при различных темп-рах. Построена по данным для различных веществ. [4] |
Существование анергии анизотропии объясняется наличиемсиин-орби-тального взаимодействия и замораживанием орбитальных моментов полем кристаллич. При повороте в кристаллах Fe, Ni, Со вектора намагниченности, обусловленного в основном спиновыми магнитными моментами, совершается работа против сил, вызванных существованием в решетке спин-орбитального взаимодействия. [5]
Ван Флек показал, что достаточным условием для замораживания орбитального момента является отсутствие орбитального вырождения; его доказательство состоит в следующем. Пусть Ф1 является собственной функцией системы, состояние которой предполагается невырожденным. Если можно пренебречь зависящими от спина взаимодействиями, то гамильтониан в, представляющий собой сумму кинетической и потенциальной энергий электронов, является действительным оператором. [6]
Этот вывод и является обобщением теоремы Ван Флека о замораживании орбитального момента. [7]
Утверждение ( а) позволяет обобщить теорему Ван Флека о замораживании орбитального момента, доказанную в гл. [8]
Поэтому приближения, сделанные в § 2, часто оказываются несправедливыми, и в этом случае имеет место слабое замораживание орбитального момента. [9]
Источником магнитокристаллической анизотропии в первую очередь следует считать спин-орбитальноо взаимодействие, которое связывает спины с частично замороженными орбитальными моментами. Замораживание орбитальных моментов вызывается сильным взаимодействием магнитных ионов с кристаллической решеткой, вернее, с кристаллическим полем, которое отражает симметрию решетки. Следовательно, посредством спин-орбитального взаимодействия осуществляется косвенное влияние решетки на спины электронов. [10]
 |
Поглощение электромагнитной энергии при парамагнитном резонансе. [11] |
В парамагнитных кристаллах на парамагнитный ион действует кристаллическое электрическое поле. Это приводит к подавлению или замораживанию орбитального момента. [12]
Если поместить ион в кристаллическое поле, представляющее собой неоднородное электрическое поле с низкой симметрией, произойдет изменение орбитального момента электронов; орбиты изменят свое положение в пространстве и вместе с тем изменится и проекция LZJ которая вследствие этого перестает быть интегралом движения. Это и есть не что иное, как замораживание орбитального момента. Происходит, однако, изменение знака ( Lz, так что рассматриваемое состояние оказывается по крайней мере дважды вырожденным, что противоречит первоначально сделанному предположению. [13]
В случае же, когда не учитывается спин-орбитальное взаимодействие, вычисление этих величин для основного состояния, изображенного на фиг. Исчезновение ( Lz) в присутствии кристаллического поля - хорошая иллюстрация эффекта, который называется замораживанием орбитального момента. [14]
Мп и Сг свидетельствуют о том, что происходит значительное уменьшение орбитального момента. С другой стороны, в системе Fe2: MgO имеет место только слабое ( порядка 0 8) замораживание орбитального момента, которое может быть обусловлено ковалент-ностью. Возможно, что это отсутствие ян-теллеровского замораживания является результатом стабилизирующего влияния спин-орбитального взаимодействия, рассмотренного в § 9 этой главы. Экспериментальное значение g 3 30 в Fe2: CaO означает, что орбитальный момент уменьшается в 0 60 раз. Причиной такого уменьшения может быть либо более сильное ян-теллеровское взаимодействие, либо большая, чем в Fe2: MgO, ковалентность. [15]
Страницы: 1 2