Невесомый вал

Cтраница 1

Невесомый вал с сосредоточенной массой гщ считается жестким. [1]

Схемы упругого невесомого вала с одной-двумя точечными массами применяются при расчете маломощных электрических машин. [2]

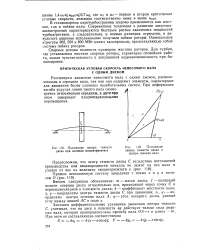Положение центра тяжести диска при наличии эксцентриситета. [3]

Рассмотрим движение невесомого вала с одним диском, расположенным в середине вала, так как оно содержит элементы, характерные для движения более сложных колебательных систем. При деформации изгиба упругая линия такого вала симме - л трична относительно середины, а диск при этом совершает плоскопараллельные перемещения. [4]

Несколько дисков на невесомом валу. Рассмотрим следующий простой пример ( фиг. Вал длиной 4 / нагружен двумя дисками. Каждый из них расположен на расстоянии / от ближайшей опоры. [5]

Это и есть дифференциальное уравнение крутильных колебаний невесомого вала при наличии одного инерционного маховика. [6]

Величину момента внутренних сил М легко, в случае невесомого вала, выразить через углы фг и фг. [7]

Тяжелый маховик силой тяжести G 5 кн, выполненный в форме обода, насажен на вертикальный невесомый вал, укрепленный в подшипниках. [8]

Крепления диска на валу - к определению критических скоростей. [9]

На рис. 24 приводятся полученные на основании соотношения ( 111) формулы для определения критической скорости невесомого вала при различных способах закрепления его в опорах и местах расположения диска на нем. [10]

Основные свойства неуравновешенных вращающихся систем отчетливо проявляются на примере колебаний шарнирно опертого вращающегося с постоянной угловой скоростью гибкого невесомого вала с одним неуравновешенным диском массы т в середине пролета. [11]

Физически такая замена означает, что ротор представляется в виде п дисков ( масс), насаженных на тонкий невесомый вал. В этом случае координатами вектора у являются прогибы вала ротора в местах посадки дисков, вектора е - эксцентриситеты этих дисков, а элементы матрицы А представляют собой произведения статических коэффициентов влияния и масс соответствующих дисков. [12]

Формула ( 1), приводимая во многих справочниках ( см., например, [3]), выведена для невесомого вала и сосредоточенной точечной массы посредине пролета и является, конечно, грубо приближенной. [13]

Для большей ясности изложения мы начнем с рассмотрения самого простого случая ( рис. 1), когда имеются два шкива / и / /, соединенных упругим невесомым валом АВ. [14]

Отсюда мы можем вывести следующее правило для вычисления числа колебаний в случае неравных шкивов: одну треть момента инерции вала делим в отношении, обратном 9j и 92; полученные величины прибавляем к моментам инерции шкивов и дальнейшие вычисления ведем по формулам, выведенным для случая невесомого вала. [15]

Страницы: 1 2