Принцип - лежандр
Cтраница 1
Принцип Лежандра требует, чтобы сумма квадратов отклонений отдельных измерений от их центра ( или от истинного размера измеряемой величины) была минимальной. [1]
Зато принцип Лежандра благодаря в первую очередь трудам Гаусса, а затем выдающихся русских математиков Чебышева и Маркова получил настолько обстоятельное развитие, что его применение в огромном диапазоне практических задач может считаться вполне освещенным. [2]
Особое развитие получил принцип Лежандра при решении обратной задачи, когда форма зависимости между измеренными величинами неизвестна и мы ищем ее из измерений. Совершенно очевидно, что это возможно лишь при избыточном числе измерений, когда ошибки отдельных измерений гасятся их численностью. [3]
Способ наименьших квадратов опирается на принцип Лежандра: определяются такие значения неизвестных, при которых сумма квадратов невязок е; наименьшая. [4]
Тот же результат дает и принцип Лежандра. [5]
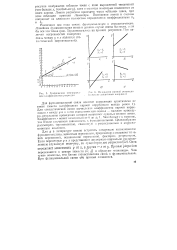 |
Графическая интерпретации коэффициентов регрессии.| Положения прямой регрессии в системе декартовых координат. [6] |
Линия регрессии проведена через облако точек, при этом соблюден принцип Лежандра. [7]
Переходя к практической стороне, нужно прежде всего отметить, что принцип Лежандра, детально разработанный главным образом Гауссом, получил в литературе гораздо большее развитие, чем принцип Лапласа. Можно отметить, что даже сам Лаплас, подчеркивая идейное преимущество медианы перед средним арифметическим, констатировал наличие известных формальных трудностей при использовании медианы в случае измерения двух и более величин. [8]
Решение линейных равноточных условных уравнений производится по способу наименьших квадратов, опирающемуся на принцип Лежандра: определяются такие значения неизвестных, при которых сумма квадратов невязок е - наименьшая. Практические указания о вычислениях по способу наименьших квадратов имеются в курсах математической статистики и специальных работах, посвященных этому - методу. [9]
Мы отыскиваем такую форму этой связи, которая при достаточной общности давала бы наилучшие возможности для применения к ней принципа Лежандра. [10]
Требование к совокупности неизвестных, чтобы она обращала в минимум сумму квадратов невязок для избыточной системы (4.81), называется принципом наименьших квадратов или принципом Лежандра. Мы видим, что совокупность значений a. [11]
Йод эту общую схему можно подвести также простейший частный случай, когда т 0 и имеется лишь один искомый параметр GO, который будет равен среднему значению, согласно принципу Лежандра, и медиане, согласно принципу Лапласа. [12]
Но совершенно ясно, что возведение отклонений в квадрат отнюдь не является единственным возможным способом избавиться от знаков отклонений. Тогда по аналогии с принципом Лежандра, изложенным в предыдущем параграфе, возникает другой принцип и ставится подобная задача отыскания центра, от которого сумма модулей будет минимальной. [13]
Обычно именно благодаря наглядности графика получаем первую возможность установить форму связи. Дальнейший же ход процесса отыскания этой формы зависит от принятия определенного руководящего принципа. Поэтому предыдущее изложение вынуждает нас в дальнейшем остановиться на одном лишь принципе Лежандра, поскольку принцип Лапласа, при всех его достоинствах, а иногда и преимуществах, практически далее линейных зависимостей до сих пор не был продвинут. [14]
Эти три одинаково недосказанных и недоказуемых положения практически почти всегда оправдываются, хотя это почти, подчеркивающее их ограниченность, побуждает излагать их в критическом разрезе. Тогда оказывается, что медиана имеет такое же, а иногда и большее право считаться центром распределения, как и среднее арифметическое. Мало того, оказывается, что постулат Гаусса о наибольшей вероятности среднего арифметического оправдывается лишь тогда, когда среднее совпадает с медианой, так как нормальное распределение может иметь силу лишь при достаточной малости отклонений по сравнению с измеряемой величиной. И, накоцец, известно, что равноправный принципу Лежандра принцип Лапласа, ставящий на место суммы квадратов отклонений суммы их модулей, если и не получил большого развития, то только потому, что математические операции, связанные с ним, оказались более громоздкими. Это чисто практическое соображение, конечно, отнюдь не подрывает доверия к принципу Лапласа в теоретическом смысле. [15]
Страницы: 1