Принцип - расщепление
Cтраница 1
Принцип расщепления состоит в разбиении трудной и длинной теоремы на маленькие и более простые частные случаи с последующим доказательством путем отдельного рассмотрения каждого случая. Правило расщепления, содержащееся в методе Девиса и Патнема, рассматривалось также в § 4.6. Метод Девиса и Патнема определен только для основных дизъюнктов. [1]
 |
Тетраэдрмческое расположение четырех отрицательных зарядов вокруг катиона Мт по отношению к осям координат, которые можно использовать для идентификации d - орбиталей. [2] |
Этот принцип расщепления, при котором алгебраическая сумма всех энергетических смещений всех орбиталей равна нулю, называют сохранением центра тяжести набора уровней. Правило сохранения центра тяжести носит достаточно общий характер и справедливо для любых типов расщепления, если вызывающие его силы являются чисто электростатическими и если набор расщепляющихся уровней сильно удален по энергии от всех других наборов, с которыми он мог бы взаимодействовать. [3]
Развитие принципов расщепления разностного оператора на уравнения массопереноса ( а также, при необходимости, и на граничные условия) приводит к методу главных направлений [12 ], причем в общем случае он может сочетаться с криволинейной координатной сеткой, учитывающей направление фильтрационного потока. Очевидным преимуществом этого метода является разомкнутость системы уравнений по направлениям, чем, в частности, устраняется доминирование - в смысле интенсивности переноса - одного направления над другим, т.е. доминирование одних членов над другими в рамках одной матрицы. Ошибки округления при решении матричных уравнений резко снижаются из-за уменьшения размеров матриц. [4]
Согласно принципу расщепления отдельные члены ( или комплексы), входящие в уравнение, можно реализовать порознь на различных промежуточных этапах. Это-естественно, упрощает построение и исследование аппроксимирующих схем. [5]
В общем случае, согласно принципу расщепления, существует морфизм /: X - X ( последовательность проективных расслоений), такой, что f E содержит флаг требуемого вида. [6]
Алгоритм решения системы (2.2) - (2.9) основан на принципах расщепления по физическим процессам и линеаризации. Решение системы линеаризованных разностных уравнений проведено методом раздельных прогонок с организацией совокупности итерационных процессов по нелинейности. Спектр излучения рассчитывается в многогрупповом приближении. В каждой группе при заданных значениях плотности и температуры решается уравнение переноса (2.2) и определяются групповые коэффициенты квазидиффузии Dp и граничного условия Ср. Затем для каждого спектрального интервала ( группы) решаются уравнения квазидиффузии (2.4), (2.5) и определяются групповые значения плотности Up и потока Wp энергии излучения. Уравнения (2.2), (2.4), (2.5) объединены в одном итерационном процессе, после окончания которого полученные групповые функции плотности и потока излучения приближенно описывают спектр излучения, эти функции в последующем используются для усреднения уравнений квазидиффузии по всему спектру. [7]
При скрещивании форм, различающихся более чем по двум парам генов, принцип расщепления остается тем же, но оно усложняется. [8]
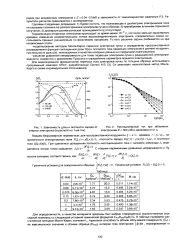 |
Зависимость дозы и плотности заряда от [ IMAGE ] Нестационарный ток при облучении. [9] |
Термализация вторичных электронов происходит за время менее 10 - 10 с, что много меньше характерного времени изменения воздействующего потока высокоэнергетических электронов, следовательно можно использовать принцип расщепления по физическим процессам. [10]
Пусть по-прежнему / - одно из тел R, С, Н, fe - теория когомодогий, удовлетворяющая требуемым выше условиям. Принцип расщепления: для произвольного векторного ( в смысле F) расслоения над В существуют пространство В и отображение /: Я - В, для к-рых расслоение / над В распадается в прямую сумму одномерных расслоений, и гомоморфизм /: h ( В) - h ( В1) мономорфен. [11]
Каждый из этих путей, при всех достоинствах, сопряжен с серьезным усложнением численной схемы и / или потерей однородности ( универсальности), что не позволяет отказываться от поисков альтернатив для МКР и МКЭ. Наиболее жизнеспособная из таких альтернатив - метод характеристик в сочетании с принципом расщепления разностного оператора. [12]
Прежде чем начинать систематическое исследование топологических действий компактных связных групп Ли на ациклических когомологических многообразиях с точки зрения теории когомологий, естественно философски осмыслить и проанализировать с технической точки зрения классическую теорию линейных представлений компактных связных групп Ли, созданную в прекрасных и глубоких работах И. Картана о максимальных торах, которая позволяет свести классификацию линейных представлений компактных связных групп Ли к аналогичной задаче для их максимальных торов. Если мы захотим теперь применить опыт, приобретенный при изучении линейного случая, в более общей ситуации топологических групп преобразований, то решающий шаг будет состоять в том, чтобы заменить расщепление линейных действий торов каким-то видом расщепления для топологических действий. Интересно отметить, что так называемый принцип расщепления в теории характеристических классов векторных расслоений использует как раз указанное выше линейное расщепление для получения важного расщепления характеристических классов. В этом параграфе мы покажем, что, хотя о расщеплении топологических действий тора на ациклических многообразиях на геометрическом уровне не может быть и речи, наличие расщепления на уровне характеристических классов действительно можно доказать. [13]
Дальнейшим шагом на пути к определению структуры белков и пептидов является определение концевых групп. N-Концевой обозначают ту аминокислоту, которая имеет в пептидной цепочке свободную а-амино-группу, С-концевой обозначают ту, которая имеет свободную карбоксильную группу. Для определения концевых аминогрупп служат различные методы; некоторые из них будут приведены далее. В последнее время было разработано несколько методов, основанных па принципе постепенного расщепления пептидов. Эти методы позволяют определить порядок чередования аминокислот в одной пробе исследуемого пептида. [14]
Напомним, что геометрическое поведение групп преобразований изучается в рамках современной топологии в следующих двух естественных ситуациях: ( i) топологические действия групп Ли ( или, более общо, топологических групп) на топологических многообразиях ( соотв. Как обычно, и в топологическом, и в дифференцируемом вариантах, имеются как локальная, так и глобальная теория. В локальной теории изучается геометрическое поведение топологического ( соотв. В случае компактных дифференцируемых групп преобразований теорема о дифференцируемом срезе ( см. теорему 1.5) показывает, что локальную теорию можно полностью свести к изучению представления группы Gx в пространстве нормальных векторов. Эта локальная линейность действия и есть как раз главная причина того, что компактные дифференцируемые группы преобразований гораздо правильнее устроены и технически более доступны для изучения, чем некомпактные или топологические группы. Это обстоятельство значительно усложняет локальную теорию топологических компактных групп преобразований. IV ( примененные к когомологическим сферам и ациклическим многообразиям) как некоторый принцип расщепления. Затем мы введем геометрическое обобщение системы весов, которое во многих отношениях служит действенной заменой локальной линейности при изучении топологических компактных групп преобразований. [15]
Страницы: 1