Принцип - франк
Cтраница 4
Следовательно, принцип Франка - Кондова можно применить и к химическим реакциям. В соответствии с этим принципом реагирующие молекулы перед перегруппировкой электронов должны находиться в благоприятном для этого положении: изменения ориентации за очень малое время перехода электронов невозможны. [46]
Как формулируется принцип Франка - Кондона для вероятности электронных переходов. [47]
Классическое обоснование принципа Франка - Кондона. В процессе возбуждения грузик остается неподвижным, а величина колебательной энергии зависит от относительного положения кривых потенциальной энергии. [48]
Квантовое обоснование принципа Франка - Кондова. Самый сильный переход происходит в состояние, с которым наинизший колебательный уровень нижнего состояния имеет наибольшее перекрывание; он показан жирной линией. Слева дан соответствующий спектр. [49]
Квантовомеханическое обоснование принципа Франка - Кон-дона связано с рассмотрением перекрывания колебательных волновых функций двух электронных состояний. [50]
Кнантовомеханическое обоаювание принципа Франка - Кондона. [51]
Необходимость выполнения принципа Франка - Кондона для перехода электрона обусловливает следующий механизм элементарного акта разряда. В этих условиях оказывается возможным кван-товомеханический ( туннельный) переход электронов из металла на реагирующую частицу. Если такой переход осуществляется, то система переходит на конечный терм и релаксирует по нему в равновесное состояние. Точка пересечения термов может быть реализована лишь при классическом поведении медленной подсистемы. В противном случае уровень энергии, отвечающий точке пересечения, может оказаться запрещенным. Таким образом, при делении системы на быструю и медленную подсистемы необходимо выполнять условие, по которому медленная подсистема должна одновременно являться и классической подсистемой. Границей такого деления является величина kT / hzx 4 - 1013: частицы с частотами колебаний ox kT / fl относят к медленной подсистеме, а с частотами a kT / fi - к быстрой. [52]
Необходи-мость выполнения принципа Франка - Кондона для перехода электрона обусловливает следующий механизм элементарного акта разряда. В этих условиях оказывается возможным квантовомеханический ( туннельный) переход электронов из металла на реагирующую частицу. Если такой переход осуществляется, то система переходит на конечный терм и релаксирует по нему в равновесное состояние. [53]
Необходимость выполнения принципа Франка - Кондона для перехода электрона обусловливает следующий механизм элементарного акта разряда. В этих условиях оказывается возможным кван-товомеханический ( туннельный) переход электронов из металла на реагирующую частицу. Если такой переход осуществляется, то система переходит на конечный терм и релаксирует по нему в равновесное состояние. Точка пересечения термов может быть реализована лишь при классическом поведении медленной подсистемы. В противном случае уровень энергии, отвечающий точке пересечения, может оказаться запрещенным. Таким образом, при делении системы на быструю и медленную подсистемы необходимо выполнять условие, по которому медленная подсистема должна одновременно являться и классической подсистемой. Границей такого деления является величина kT / hz & 4 - 1013: частицы с частотами колебаний ox kT / fl относят к медленной подсистеме, а с частотами a kT / fi - к быстрой. [54]
Необходимость выполнения принципа Франка - Кондона для перехода электрона обусловливает следующий механизм элементарного акта разряда. В этих условиях оказывается возможным кван-товомеханический ( туннельный) переход электронов из металла на реагирующую частицу. Если такой переход осуществляется, то система переходит на конечный терм и релаксирует по нему в равновесное состояние. Точка пересечения термов может быть реализована лишь при классическом поведении медленной подсистемы. В противном случае уровень энергии, отвечающий точке пересечения, может оказаться запрещенным. Таким образом, при делении системы на быструю и медленную подсистемы необходимо выполнять условие, по которому медленная подсистема должна одновременно являться и классической подсистемой. Границей такого деления является величина kT / hzx 4 - 1013: частицы с частотами колебаний ox kT / fl относят к медленной подсистеме, а с частотами a kT / fi - к быстрой. [55]
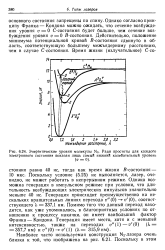 |
Энергетические уровни молекулы N2. Ради простоты для каждого электронного состояния показан лишь самый нижний колебательный уровень. [56] |
Однако согласно принципу Франка - Кондона можно ожидать, что сечение возбуждения уровня о 0 С-состояния будет больше, чем сечение возбуждения уровня о 0 В-состояния. Действительно, положение минимума потенциальной кривой В-состояния сдвинуто в область, соответствующую большему межъядерному расстоянию, чем в случае С-состояния. [57]
Квантовомеханическое рассмотрение подтверждает принцип Франка - Кондона: вертикальные переходы на диаграмме потенциальной энергии действительно оказываются наиболее вероятными. Напомним, что осциллятор, соответствующий реальной молекуле, никогда не бывает в состоянии покоя, а вероятность распределения колеблющихся масс на нулевом колебательном уровне ( v 0) определяет область возможных расстояний между ядрами в этом состоянии. [58]
Страницы: 1 2 3 4