Формальная запись

Cтраница 1

Формальная запись дифференциала в обоих случаях одинакова. Говорят, что форма первого дифференциала инвариантна относительно замены переменных. [1]

Подобная формальная запись иногда применяется для диффузионных потоков. [2]

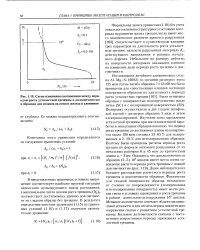Схема изменения соотношения между периодом роста усталостной трещины и долговечностью в образцах для сплавов на основе железа и алюминия. [3]

Формальная запись уравнения (1.18) без учета локального влияния структурного состояния материала на развитие малых трещин, когда имеет место немонотонное развитие процесса разрушения [100], свидетельствует о существенном влиянии трех параметров на длительность роста усталостных трещин: вязкости разрушения материала Кс, действующего напряжения и размера начального дефекта. Небольшие по размеру дефекты на поверхности материала оказывают влияние на изменение доли периода роста трещины в долговечности. [4]

Формальная запись соответствующих выражений не представляет труда, но вычисление интегралов затруднительно. Приемы вычисления указаны в работе [5], гл. [5]

Формальную запись процесса обработки информации, которая задает точное предписание о выполнении в строго определенном порядке некоторого комплекса операций для решения задач определенного класса, принято называть алгоритмом. [6]

Естественной формальной записью многих задач проектирования устройств АСУ являются дискретные экстремальные задачи. [7]

В формальной записи описанные выше задачи оптимизации надежности выглядят следующим образом. [8]

В формальной записи (4.21) символы имеют следующий смысл: А обозначает операцию логического умножения ( конъюнкции), Я есть квантор существования. [9]

Дадим формальную запись описанного выше ( модифицированного) алгоритма на языке Сетл. [10]

Переходя к формальной записи этого утверждения, устанавливаем справедливость леммы. [11]

Для удобства формальной записи можно считать, что в уравнение (1.4.7) входят концентрации с всех веществ, участвующих в реакции. При этом порядок реакции по тому веществу, которое в уравнение не входит, положим равным нулю. [12]

Рассмотрим более подробно формальную запись условия единства измерений относительно случайной погрешности. Установленные границы для случайной погрешности, которые фигурируют в определении понятия единство измерений, по существу представляют поле допуска для погрешности [ е0, вы ], где е00, e0i0, Те - допуск поля допуска. [13]

Это и есть формальная запись точного решения задачи. Хотя рассмотренный пример и является впечатляющим, однако для осуществления такого процесса нам необходимо вычисление оператора Л -, а это задача, эквивалентная по трудности исходной задаче. [14]

Уравнение (1.4.31) представляет собой формальную запись векторного дифференциального уравнения Ито, которое эквивалентно некоторому стохастическому интегральному уравнению. [15]

Страницы: 1 2 3 4