Заполнение - матрица
Cтраница 1
Заполнение матриц В [ Т и В2Т происходит согласно представлению линеаризованных ( относительно конфигурации т) деформаций через приращения перемещений. [1]
Заполнение матриц производится следующим образом. [2]
Заполнение матриц взаимосвязи осуществляется также в режиме диалога на основе составления и решения логического уравнения специального типа, которое назовем характеристическим. Уравнение составляется следующим образом. Если Мал и Мвв содержат матрицы взаимосвязи, то они заполняются в соответствии с приведенным ниже алгоритмом. [3]
Заполнение матрицы U происходит по следующему алгоритму. [4]
После заполнения матрицы накладывают пуансон, и подготовленную таким образом прессформу устанавливают между плитами пресса и создают давление, обеспечивающее полное закрытие прессформы. [5]
После заполнения матрицы порошок прессуется под давлением одного или нескольких пуансонов. [6]
 |
Конфигурация подкуба пер - [ IMAGE ] Конфигурация подкуба вто-вого порядка рого порядка. [7] |
Для заполнения матрицы Карно в отличие от рассмотренного выше примера используют следующий способ. По релейной функции, заданной с помощью набора десятичных номеров комбинаций значений входных переменных при известном базисе, определяют веса столбцов и строк. [8]
Для заполнения матрицы необходимо получить по крайней мере по одному решению из каждой ЗРЭР. [9]
Для заполнения матрицы Ех необходимо произвести вычитание п2 раз. [10]
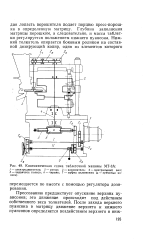 |
Кинематическая схема таблеточной машины МТ-ЗА. / - электродвигатель. 2 - ротор. 3 - ворошитель. 4 - центральный вал. 5 - червячное колесо. 6 - червяк. 7 - муфта включения ( z - зубчатые колеса. [11] |
Глубина заполнения матрицы порошком, а следовательно, и масса таблетки регулируется положением нижнего пуансона. [12]
Коэффициент заполнения матрицы А характеризует исходную разреженность матрицы. Рассмотренные выше примеры показывают, что в процессе исключений Гаусса и LU-разложения в матрице появляются новые ННЭ. [13]
Порядок заполнения матрицы понятен из приведенного выше матричного уравнения и особых пояснений не требует. [14]
Пример заполнения матрицы для области с девятью узлами, представленной на рис. 3.14, показан на рис. 3.15, в котором символом х отмечены ненулевые коэффициенты. [15]
Страницы: 1 2 3 4