Вальд

Cтраница 1

Вальд и другие обобщили теорему фон Неймана для множеств X и Y, принадлежащих некоторым бесконечно-мерным пространством. [1]

Вальд доказал [2] полную определенность бесконечных антагонистических ЕТ Р % вторых пространства стратегий игроков условно компактны в естествени. Оаже установил, что если вместо условной компактности пространств стратегий потребовать их компактность, то эта теорема может быть усилена: вместо полной определенности игры можно утверждать существование оптимальных стратегий у игроков. При всей своей кажущейся наглядности этот результат является весьма тонким и нетривиальным. [2]

Вальд также доказал, что его критерий существенно выгоднее ( по среднему числу наблюдений), чем наилучший из классических критериев - критерий Неймана-Пирсона. [3]

Вальд использует приведенные выше результаты, чтобы создать метод практического сравнения двух эмпирически полученных последовательностей испытаний ( например, результаты работы двух машин) в целях выбора той, которая обещает большую вероятность успеха. [4]

Вальд использует приведенные выше результаты, чтобы создать практический метод сравнения двух эмпирически полученных последовательностей испытаний ( например, результаты работы двух машин) для выбора той, в которой вероятность успеха больше. [5]

Вальда и обеспечивает минимаксность найденного правила. [6]

Вальда) - это пессимистический по своей сути критерий, потому что принимается во внимание только самый плохой из всех возможных результатов каждой альтернативы. [7]

Вальда имеет силу лишь при v О ( & - - 2К) Еач, что имеет место лишь с вероятностью, большей, чем 1 - 0 ( К-1) - Поэтому, чтобы в подавляющем числе последовательных процедур мы имели право надежно пользоваться аппроксимацией Вальда для распределения числа испытаний, К должно быть велико. [8]

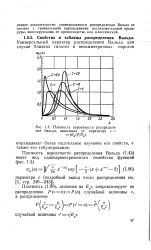Плотность вероятности распределения Вальда, зависящая от параметра с. [9]

Вальда не связано с тривиальными вырождениями последовательной процедуры, нивелирующими ее превосходство над классической. [10]

Вальда) - это пессимистический по своей сути критерий, потому что принимается во внимание только самый плохой из всех возможных результатов каждой альтернативы. [11]

Вальда, Сэвиджа и некоторые другие. [12]

Вальдом [58] было установлено, что при п - - оо оптимальное число К. [13]

Вальдом установлено, что если отношение рв / рн В, то контролируемая партия может быть принята по качеству, а если рв / рн А, то отклонена. [14]

Вальдом [1] было предложено использовать в качестве показателя сложной последовательной процедуры функцию риска. [15]

Страницы: 1 2 3 4