Жидкое заполнение
Cтраница 1
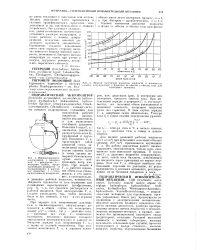 |
Пненмогидранлнч. аккумулятор с диафрагмой. / - диафрагма. 2 - металлич. шайба, предохраняющая диафрагму от продавливают в расход-нос отверстие. з - утолщение ( поясок диафрагмы. [1] |
Жидкое заполнение часто применяется в силовых трансформаторах, дросселях, конденсаторах и др. высоковольтных и мощных устройствах. Оно улучшает охлаждение, давая возможность значительно 200 уменьшать размеры аппаратуры, а ол также работать с повыш. Применение жидкого заполнения 120 имеет сноп отрицат. [2]
Жидкое заполнение часто применяется в силовых трансформаторах, дросселях, конденсаторах и др. высоковольтных и мощных устройствах. Оно улучшает охлаждение, давая возможность значительно уменьшать размеры аппаратуры, а также работать с иовыпг. Применение жидкого заполнения имеет свои отрицат. [4]
 |
Расчетные схемы динамических систем с жидким. [5] |
Подробное исследование динамики я-массовой системы с жидким заполнением было выполнено в работах [27, 28, 86], где рассматривались линейные, нелинейные и параметрические системы при детерминированных и случайных внешних нагрузках. [6]
Рассмотрим теперь колебания п-массовой системы с жидким заполнением как системы с бесконечно большим числом степеней свободы. [7]
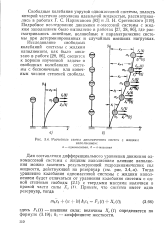
Число степеней свободы любой динамической системы с жидким заполнением равно бесконечности. Даже одномассовая система в отличие от системы с жесткой массой имеет бесконечное число степеней свободы за счет жидкого наполнения. В дальнейшем будут приняты следующие расчетные схемы, которыми можно моделировать очень многие конструкции аппаратов химического машиностроения, оборудования и сооружений. На рис. 3.4, а показана одномассовая схема, а на рис. 3.4, б п-массовая схема, число степеней свободы которых равно бесконечности. Такие динамические расчетные схемы удобны для математического анализа и позволяют достаточно полно учесть все особенности конструкции. [8]
 |
Расчетные i модели сооружений, несущих резервуары. [9] |
Число степеней свободы любой динамической системы с жидким заполнением равно бесконечности. Даже одномассовая система ( рис. 5) в отличие от системы с жесткой массой имеет бесконечное число степеней свободы за счет жидкого заполнения. Рассмотрим одномассовую ( рис. 5, а) и л-массовую ( рис. 5, б) расчетные модели, которыми можно моделировать очень многие конструкции аппаратов химического машиностроения, оборудования и сооружений. Такие динамические расчетные модели удобны для математического анализа и позволяют достаточно полно учесть все особенности конструкции. [10]
Подробное исследование динамики - массовой системы с жидким заполнением было выполнено автором работ [53, 54], которые рассматривали линейные, нелинейные и параметрические системы при детерминированных и случайных внешних нагрузках. [11]
В настоящей главе будет рассмотрена задача о колебании одномассовой нелинейной системы с жидким заполнением и твердыми массами при действии случайной нагрузки. Сначала рассмотрим частный случай нелинейности - безынерционную нелинейность степенного вида, а затем исследуем систему с нелинейностью общего характера: нелинейная упругость, нелинейное затухание и нелинейная инерционность. Решения этих задач будут получены приближенными методами, так как точных математических методов исследования нелинейных систем при случайных возмущениях в настоящее время нет. [12]
ДЛЯ расчетов динамических Характеристик в резонансном режиме или когда на тело с жидким заполнением действуют силы, представляющие случайный во времени процесс. [13]
Эти уравнения являются точными для определения частот и форм собственных колебаний системы с жидким заполнением. [14]
В книге значительное место уделено исследованию колебаний жидкости в резервуарах и упругих систем с жидким заполнением. [15]
Страницы: 1 2