Проверка - математическая модель
Cтраница 1
Проверка математической модели на адекватность проведенная по результатам работы промышленной установки, показали что средняя за цикл коксования расчетная температура верха реактора отличается от экспериментальной на 0 5 - 1 0 С. [1]
Проверка математической модели на адекватность реальному объекту производится для выяснения того, требуется ли коррекция модели. Она осуществляется путем сравнения экспериментального профиля концентраций по высоте колонны с рассчитанным по модели. [2]
Для проверки математической модели были проведены экспериментальные исследования растворимости АСПО. [3]
При проверке математической модели использовались данные Дергарабедяна [5], представленные на фиг. Кружочками указаны данные, полученные из измерений с кадров высокоскоростной киносъемки, а кривая построена путем интерполяции расчетных результатов, представленных на фиг. Интерполяция легко осуществима, так как кривые являются параболами. [4]
Математическая статистика занимается как статистическим описанием результатов опытов или наблюдений, так и построением и проверкой подходящих математических моделей, содержащих понятие вероятности. Ее методы расширяют возможности научного предсказания и рационального принятия решения во многих задачах, где существенные параметры не могут быть известны или контролируемы с достаточной точностью. [5]
КПД относительно рассчитанных; 6) профиль содержаний спирта, рассчитанный по модели; 7) результат проверки математической модели на адекватность; 8) результат выполнения индивидуального задания. [6]
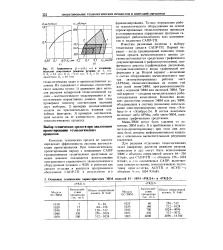 |
Зависимость Q p ( Sf ( а и изменение областей допустимых режимов резания от. ( б. 1 6 / 0 2 мм. 2 8 0 15 мм. 3 5 / 0 1 мм ( для диаметров Df 60 мм. [7] |
Их оценивают с помощью статистического анализа путем: 1) сравнения двух методов решения конкретной технологической задачи - математического моделирования и использования нормативных данных; при этом проверяют гипотезу соответствия значений двух выборок; 2) проверки математической модели на чувствительность влияния случайных факторов; 3) проверки математической модели на ее адекватность реальному технологическому процессу. [8]
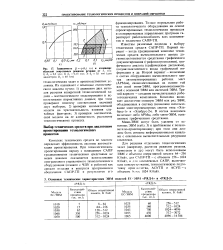 |
Зависимость Q p ( Sf ( а и изменение областей допустимых режимов резания от. ( б. 1 6 / 0 2 мм. 2 8 0 15 мм. 3 5 / 0 1 мм ( для диаметров Df 60 мм. [9] |
Их оценивают с помощью статистического анализа путем: 1) сравнения двух методов решения конкретной технологической задачи - математического моделирования и использования нормативных данных; при этом проверяют гипотезу соответствия значений двух выборок; 2) проверки математической модели на чувствительность влияния случайных факторов; 3) проверки математической модели на ее адекватность реальному технологическому процессу. [10]
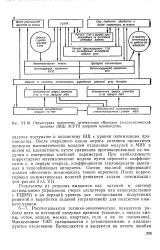 |
Структурная подсистема оптимизации Выпарка электролитической щелочи ( ВЩ АСУТП хлорного производства. [11] |
После очередного цикла опроса датчиков проводится проверка математических моделей отдельных модулей и МВУ в целом на адекватность путем сравнения прогнозированных по модулям и измеренных значений параметров. При необходимости корректируют математические модели путем пересчета коэффициентов и, в первую очередь, коэффициентов теплопередачи выпарных и теплообменных аппаратов. Состав входной информации должен обеспечить возможность такого пересчета. После корректировки математических моделей решаются задачи оптимизации ( см. раздел 3 гл. [12]
Используемые для решения задач оптимизации математические модели ТП и производств зачастую нуждаются в систематической или эпизодической проверке и коррекции. Эту функцию в АСУ выполняют специальные алгоритмы адаптации и проверки математической модели. [13]
Эти исследования могут служить надежным источником данных при построении и проверке математической модели прихвата. [14]
Эти возражения не лишены оснований. Однако в подобных математических стендах может быть использовано много стандартных ( унифицированных) блоков ( алгоритмов), общих для всех стендов проверки математических моделей. Стандартизация и многократное использование математического стенда являются тем экспериментом, той практикой, которая позволит устранить имеющиеся ошибки и обеспечит работоспособность стенда. Кроме того, моделирование исходных параметров и проверка правильности математической модели по ним существенно снизят вероятность того, что ошибка останется необнаруженной. Это объясняется тем, что совпадение ошибок одного типа как в стенде, так и в математической модели ( а именно в этом случае они останутся необнаруженными) можно считать достаточно редким событием. [15]
Страницы: 1 2