Проверка - точность - решение
Cтраница 1
Проверка точности решения и оценка погрешностей осуществляются путем сравнения решения, выдаваемого АВМ, с точным решением, получаемым аналитически или числ. [1]
Проверка точности решения н оценка погрешностей осуществляются путем сравнения решения, выдаваемого АВМ, с точным решением, получаемым аналитически или чнсл. [2]
Для проверки точности решения нами была избрана задача, ллощая аналитическое решение. [3]
Для проверки точности решения повторим его, разбив провод на и 10 частей. [4]
С целью проверки точности решения задачи было предпринято аналитическое ее решение с соответствующими числовыми расчетами для случая деления стержня на 10 частей при значении начальной скорости UQ 0.05. Этот вариант легко считается вручную, так как пластические деформации в процессе удара распространяются только на три первых стерженька. [5]
Необходимо отметить, что, несмотря на полезность проверки точности решения задач на частых сетках, этот способ имеет ограниченную область применения. Действительно, расчет сложных течений обычно ведется на пределе возможностей ЭВМ, а вычисления на более грубых сетках могут дать искаженные результаты. [6]
При этом а const j - const2 задается как параметр для проверки точности решения и завершения вычислений. [7]
При этом А - const, - const2 задается как параметр для проверки точности решения и завершения вычислений. [8]
При этом AV FJ ( z) - V2 ( z) задается как параметр для проверки точности решения и завершения вычислений. [9]
Стьюдента; в) выходного параметра у; г) невязок у у - УЭ, где уз - экспериментальное значение выход-лого параметра; д) достаточной дисперсии, определенной по двум формулам для проверки точности решения; с) показатели дисперсии относительного среднего значения выходного параметра; ж) РОТн - меры практической ценности уравнения регрессии. [10]
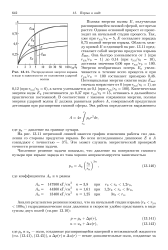 |
Распределение энергии взрыва в воде в зависимости от положения ударной. [11] |
На рис. 13.11 штриховой линией нанесен график изменения работы сил давления со стороны продуктов взрыва. Это может служить энергетической проверкой точности решения задачи. [12]
Как показали Хоффман и Ариман [9], наибольшая точность в решении задач о колебаниях прямоугольной пластинки с кр уговым вырезом при помощи метода наименьших квадратов достигается при отношении числа уравнений к числу неизвестных, близком к двум. Для подтверждения этого заключения была рассмотрена сплошная квадратная пластинка с шарнирно опертыми краями, для которой существует решение в замкнутой форме; однако собственная частота колебаний отыскивалась при помощи метода коллокации, что позволяло произвести проверку точности решения. При сохранении числа, точек коллокации обнаружено, что наилучшие результаты с точки зрения точности решения и трудностей вычислительного характера были получены при п 4 членах ряда. [13]
Заметим, что для определителя, являющегося знаменателем уравнения ( 5 - 9), существует симметрия относительно главной диагонали. Например, значения члена во втором ряду третьей колонки равно значению члена в третьем ряду второй колонки. Это свойство способствует проверке точности решения. [14]
В классической механике эта теорема была введена еще Клаузиусом. Теорема вириала выполняется только для точных решений. Отклонение от этой теоремы является одним из основных тестов для проверки точности решения. [15]
Страницы: 1 2