Проверка - устойчивость - система
Cтраница 1
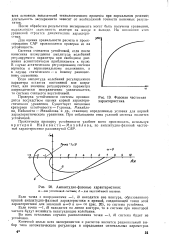 |
Фазовая частотная характеристика.| Амплитудно-фазовые характеристики. [1] |
Проверка устойчивости системы производится посредством оценки корней характеристического уравнения. Существует несколько критериев устойчивости - Гурвица, Михайлова, Найквиста - Михайлова и др., ставящих определенные условия для корней характеристического уравнения. При соблюдении этих условий система является устойчивой. [2]
 |
Амплитудно-фазовые характеристики котла и системы отопления. [3] |
Проверка устойчивости системы и критического запаздывания по Ципкину дает значение ткр около 1 5 мин. [4]
После проверки устойчивости системы переходят к построению переходного процесса, вызванного единичным ступенчатым воздействием. [5]
Рассмотрим способы проверки устойчивости систем с неподвижными узламн. Пусть необходимо определить критическую силу для системы, изображенной на фиг. Наложим на узлы 1 и 2 системы защемления ( фиг. [6]
Обычно при проверке устойчивости системы выявляют точку, в которой короткое замыкание наиболее опасно, и для нее проводят расчеты. Однако вероятность того, что короткое замыкание данного вида произойдет именно в этой точке, разумеется, значительно ниже, чем общая вероятность появления рассматриваемого вида короткого замыкания в системе. [7]
Таким образом, проверка устойчивости системы сводится к определению точки пересечения годографа вектора этой характеристики с отрицательной вещественной полуосью комплексной плоскости. [8]
Критерий Рауса - Гурвица применяется для проверки устойчивости системы с заданными параметрами. В тех же случаях, когда известны не коэффициенты, а передаточные функции разомкнутой системы, использование критерия оказывается неудобным. [9]
Алгебраические критерии Гурвица и Рауса удобны при проверке устойчивости систем до пятого-шестого порядка. Для систем высших порядков выгоднее применять частотные критерии Найквиста и Михайлова. [10]
АРУ и его постоянных времени, необходимо производить проверку устойчивости системы. [11]
При исследовании устойчивости систем автоматического управления может ставиться задача не только проверки устойчивости системы при заданных значениях ее параметров, но также и определения некоторой области изменения отдельных параметров, внутри которой система остается устойчивой. [12]
Критерий Рауса представляет правило, определяющее ряд последовательных алгебраических операций, необходимых для решения задачи проверки устойчивости системы. [13]
Если при этом переходе ни одна мощная станция не выпадает из синхронизма, то переход считается благополучным. Обычно проверка устойчивости системы производится при коротких замыканиях, происходящих в наиболее опасных в смысле возможного нарушения устойчивости точках системы при наибольшей возможной нагрузке электропередачи. В случае системы, состоящей из станции, работающей через длинную линию на шины неизменного напряжения, такая точка расположена вблизи шин станции. [14]
При выборе типа регулятора приходится искать компромиссное решение между стремлением упростить и, следовательно, удешевить систему регулирования и необходимостью обеспечить требуемое качество регулирования. Процесс подбора регулятора расчленяется обычно на три этапа: предварительный выбор, расчет настройки, проверка устойчивости системы. [15]
Страницы: 1 2