Численная проверка
Cтраница 2
В этом параграфе будут изложены результаты численной проверки теоретического анализа разностных схем газодинамики, который был выполнен в предыдущих параграфах и привел к формулировке полностью консервативных схем. Эти схемы, как отмечалось, более эффективны, чем прочие схемы, при расчете на грубых временных сетках решений, претерпевающих сильные изменения во времени и пространстве. [16]
Многоканальная формулировка проводимости предоставляет идеальное средство для численной проверки этой идеи. Неупорядоченная модель сильной связи Андерсона может быть использована для описания ( невзаимодействующей) системы. Свойства сходимости этого метода оказываются подходящими для случаев, представляющих здесь интерес. [17]
Оценки, полученные на этой основе, подвергаются численной проверке применительно к некоторым фирмам в США. [18]
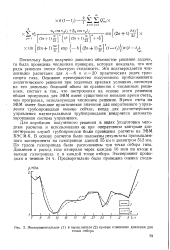 |
Экспериментальная ( 1 и вычисленная ( 2 кривые изменения давления для. [19] |
Поскольку было получено довольно объемистое решение задачи, то была проведена численная проверка, которая показала, что все ряды решения имеют быструю сходимость. Это подтверждается численными расчетами для я 8 и я 20 практических задач транспорта газа. Основное преимущество полученного приближенного аналитического решения при заданных краевых условиях, несмотря на его довольно большой объем по сравнению с численным решением, состоит в том, что построенная на основе этого решения общая программа для ЭВМ имеет существенно меньшее время счета, чем программа, использующая численное решение. Время счета на ЭВМ имеет большое практическое значение для оперативного управления трубопроводами именно сейчас, когда для диспетчерского управления магистральными трубопроводами внедряется автоматизированная система управления. [20]
Тем не менее, следует заметить, что эта гипотеза требует доказательства или более подробных численных проверок. Кроме того, заметим, что все ситуации, рассмотренные в этом разделе, относятся к вязкоупругой среде. Принципы отбора решений могут быть другими, если в среде существуют другие размазывающие механизмы ( см. разд. [21]
Это рассуждение не является, конечно, строгим и нуждается, по крайней мере, в численной проверке. [22]
Математику же, без которой он, как и большинство представителей науки Возрождения, считал недостоверным всякое знание, понимает весьма узко: для него это лишь возможность численной проверки какого-либо утверждения; математической он считал такую формулировку, которая устанавливает числовую зависимость между несколькими величинами, обычно в виде пропорции. [23]
Как известно, условия типа (1.16) являются лишь необходимыми для существования максимума функции. Численная проверка в диапазоне а 15 - 30; ц, 0 4 - н - 1Д г) 0 80 - 0 92; Р2 120 - 170 показала, что эти условия в данном случае являются также и достаточными. [24]
Этот метод разработан Чарным [47] для ограниченного пласта с постоянным давлением на контуре питания. Численная проверка решения основного уравнения для этого случая без использования специальных счетных машин практически невозможна по той причине, что в решение входит бесконечный ряд, выраженный сложными функциями Бесселя. [25]
Весьма существенным является вопрос о сходимости такого итерационного процесса, которая, очевидно, будет зависеть от операторов А к В, определяемых характером задачи ( пространственная или плоская) и типом неоднородности. Хотя численная проверка показала хорошие результаты, вопрос о сходимости метода в целом остается открытым. [26]
Поскольку из физических соображений величина циркуляции вихря Тр может быть задана произвольно, то естественно возникает вопрос, что произойдет с течением, если Re TP / v превысит Re. В работах [68, 142, 177] предпринята численная проверка теоретических результатов. [27]
В данной задаче величины Ti быстро уменьшаются по мере удаления от начального и приближения к конечному сечению. Отсюда следует, что в области, примыкающей к конечному сечению оболочки, Т1 - по (4.17) будут определяться как очень малые разности весьма больших чисел. Численная проверка подтверждает эти выводы. [28]
В подавляющем большинстве случаев уже само приближение Борна - Оппенгеймера позволяет получить очень хорошее описание реальной системы. Надежная численная проверка возможна лишь для самых малых систем, расчеты которых позволяют достичь одинаковой или даже более высокой точности, чем точность экспериментально измеряемых величин. [29]
В подавляющем большинстве случаев уже само приближение Борна - Оппенгеймера позволяет получить очень хорошее описание реальной системы. Надежная численная проверка возможна лишь для самых малых систем, расчеты которых позволяют достичь одинаковой или даже более высокой точности, чем точность экспериментально измеряемых величин. [30]
Страницы: 1 2 3