Конечный прогиб

Cтраница 1

Конечные прогибы следует определять с учетом последовательности механической обработки и характера закрепления станины на станке. Если обрабатываемая деталь, в данном случае станина, нежесткая, а крепление ее на столе жесткое и не позволяет ей перемещаться в процессе механической обработки, то в результате обработки возникнут реакции в закреплении, которые после освобождения детали вызовут ее деформацию. Допустим, слои А и Ах снимают за одну установку без перекрепления. Тогда прогибы fA и / Л, необходимо сложить с учетом их знака. Если после механической обработки по слою Ах станина освобождается, а затем проводится обработка слоя А, то прогиб по плоскости обработки А будет / д, а по плоскости Ах запишется как сумма / д и / д, с учетом знаков. [1]

Применяемый к расчету устойчивости оболочек при конечных прогибах метод последовательных нагружений ( В. В. Петров, 1959) является модификацией метода последовательных приближений. Метод игнорирования форм выпучивания при определении критических сил оболочек, предложенный сперва для линейных задач ( В. Власов, 1949), был распространен на нелинейные задачи для однородных ( А. В. Саченков, 1963; К. [2]

Граничные условия на кромках пологой оболочки при конечных прогибах формулируются аналогично краевым условиям для пологой оболочки при малых прогибах или для гибкой пластины. [3]

Условие стационарности 8 ( АЭ) 0 определяет равновесные состояния изогнутого стержня при конечных прогибах, а исследование знака второй вариации ба ( АЭ) позволяет установить, какие из равновесных состояний устойчивы. [4]

Условие стационарности б ( ЛЭ) 0 определяет равновесные состояния изогнутого стержня при конечных прогибах, а исследование знака второй вариации б2 ( ЛЭ) позволяет установить, какие из равновесных состояний устойчивы. [5]

Этот случай сам по себе не представляет особого практического интереса, но он иллюстрирует очень важный принципы конечного прогиба или большого прогиба в нелинейных задачах пластин и оболочек, получить решение для которых намного труднее. С целью проиллюстрировать эти принципы достаточно обратиться к следующему простому случаю. [6]

В отличие от степенной зависимости или зависимости гиперболического синуса использование дробно-линейного соотношения приводит к качественно новому результату - потере устойчивости при малых конечных прогибах. [7]

При деформировании лагранжевы координаты 6i, 62 будем полагать совпадающими с координатами х, у, считая деформации в плоскости ху малыми, и учитывать квадратичную нелинейность, связанную с конечным прогибом панели и произвольным сжатием элементов по толщине. [8]

Вторые слагаемые прогибов ( в приведенных ваше представлениях они пропорциональны параметру Ь) могут описывать как направленный внутрь оболочки прогиб при внешнем давлении ( который не учитывался в описываемой классической постановке задачи устойчивости), так и более важный осесимметричный направленный внутрь оболочки прогиб, который существует во всех теориях конечного прогиба, чтобы частично компенсировать нелинейные окружные деформации, обусловленные образованием волн в окружном направлении с линейными деформациями относительно кривизн в окружном направлении. [9]

В целом книга самобытна, интересна отбором материала, его нестандартным обсуждением. Разумеется, автор не обошел и рассмотрение трактовок вопросов выпучивания и конечных прогибов упруго деформируемых систем. [10]

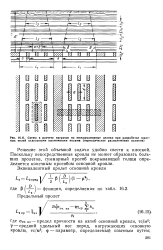Схема к расчету нагрузок на междукамериые целики при разработке шахтных полей отдельными выемочными полями ( периодическое расположение целиков. [11]

Решение этой объемной задачи удобно свести к плоской. Поскольку непосредственная кровля не может образовать больших пролетов, суммарный прогиб покрывающей толщи определяется конечным прогибом основной кровли. [12]

Таким образом, при наличии начальной неправильности, либо эксцентриситета продольной силы, либо поперечной нагрузки прогибы и ( г) растут бесконечно при F - FKp3. Если в решении учесть геометрические нелинейности, появление которых неизбежно с ростом прогибов, то каждой конечной силе соответствует конечный прогиб, аналогично тому, как это показано в § 15.6. Такое положение более соответствует истине. [13]

Полагается, что напряжения и скорости деформаций постоянны на элементе или рассматриваются как усредненные величины. Композиционные материалы при деформировании и разрушении часто не испытывают существенно больших деформаций, поэтому в данной модели учитываются квадратичная нелинейность деформаций, связанная с конечным прогибом слоев, и нелинейные деформации сжатия - растяжения по толщине панели. [14]

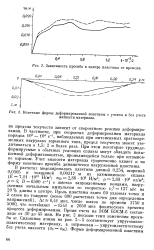Зависимость прогиба в центре пластины от времени.| Конечные формы деформированной пластины с учетом и без учета. [15]

Страницы: 1 2