Программа - вычислительная машина
Cтраница 2
По решению поставленной задачи известна лишь одна работа [4.4], в которой разработана программа вычислительной машины, определяющая ВАХ ТЭ в зависимости от вышеизложенных неоднородностей. Авторы в процессе решения делят поверхность каждого электрода на ряд прямоугольных решеток, каждой из которых приписывают постоянные по всей поверхности параметры. Предполагается, что ВАХ одного элемента деления является такой же, как и в небольшом испытуемом ТЭ при некоторых однородных условиях. Информация, касающаяся электродной поляризации, влияния температуры на поляризацию и скорость переноса воды, термические свойства охлаждающего агента, конструкция и удельные сопротивления токосъемного тракта вводятся в программу вычислительной машины как входные данные. При этом решается система уравнений, описывающих условия баланса токов и теплового баланса. К недостаткам работы относится то, что решение проводится для одномерного движения охлаждающего агента и не ясно, как перейти к решению задачи с неодномерным движением. [16]
Карточные перфораторы являются также электромеханическими устройствами и применяются для перфорации отверстий под управлением программы вычислительной машины или контроллера внешнего устройства. Скорость работы устройств считывания с перфокарт лежит в диапазоне от 300 до 1200 карта / мин. Карточные перфораторы обычно имеют меньшее быстродействие - от 60 до 500 карта / мин. [17]
В 1833 г. английский математик Чарльз Беббидж впервые сформулировал основополагающий принцип программного управления и принцип запоминаемой программы вычислительных машин, которые осуществлены в современных ЭВМ. Задуманная Беббиджем аналитическая машина должна была состоять из арифметического устройства, запоминающего устройства и устройства автоматического управления с хранением программы на перфокартах. [18]
Порядок выполнения микрокоманд в микропрограмме может быть организован так же, как выполнение последовательности команд в программе вычислительной машины. Можно иметь, например, соответствующий счетчик микрокоманд, который содержит адрес следующей микрокоманды и увеличивает его на единицу после выполнения каждой микрооперации. [19]
Так как теорема об ускорении применима ко всем мерам сложности, то ее можно применять для ускорения программ вычислительных машин. Однако такие программы обычно используются для вычисления значений функции для некоторого конечного множества значений аргумента, а не для всевозможных значений. Уменьшение асимптотического времени работы программы почти всюду - это не совсем то, в чем заинтересован вычислитель-практик. Однако теорема говорит о том, что мы не можем классифицировать функции по сложности их вычисления, так как некоторые функции не имеют внутренней минимальной сложности. То, что мы будем делать вместо этого, - это определять классы сложности и изучать их в разд. [20]
Предпотожим, что каждая функция фг - вычислима посредством некоторого множества команд Mi, MI может быть машиной Тьюринга, программой идеализированной вычислительной машины или системой уравнений. Скажем, что последовательность ( Mi) имеет допустимую геделевскую нумерацию, если таковую имеет ( фг); далее мы везде будем предполагать, что ( фг) такова. Теорема Роджерса позволяет нам предполагать ( так мы и сделаем без потери общности), что любые два класса машин ( М и ( Ti) ( оба с допустимыми геделевскими нумерациями) упорядочены так, что Мг и 7 вычисляют одну и ту же функцию фг. [21]
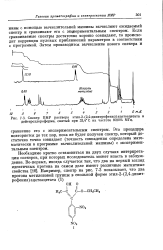 |
Спектр ПМР раствора этил-2 - ( 2 4-динитрофенил ацетоацетата в дейтерохлороформе, снятый при 33 4 С на частоте 60 004 МГц. [22] |
Эта процедура повторяется до тех пор, пока не будет получен спектр, который достаточно точно совпадает ( точность совпадения определена математически в программе вычислительной машины) с экспериментальным спектром. [23]
Таким образом, значение сигнала от токового датчика, значительно меньшее, чем утопленный нуль, может считаться недостоверным. Программа вычислительной машины может обнаружить этот факт, сравнивая цифровой отсчет с контрольной величиной. Чтобы избежать ошибок калибровки и облегчить использование АСУ при калибровке, контрольная величина должна быть немного меньше утопленного нуля; часто она составляет 75 % номинальной - величины. Контрольная величина для проверки перехода за утопленный нуль определяется пределами изменения тока на выходе датчика и коэффициентом усиления подсистемы аналогового входа, выраженным отношением машинных разрядов на миллиампер. Таким образом, контрольная величина не является функцией режима технологического процесса. [24]
Если установка не оснащена управляющей вычислительной машиной ( а в настоящее время это обычно не практикуется), то весьма желательно будет проанализировать на вычислительной машине продукцию автоматического регистратора данных. Далее, программа вычислительной машины может предусматривать проверку того, насколько хорошо полученные фактические данные совпадают с предсказаниями моделей процесса, и выдачу рекомендаций относительно изменения коэффициентов уравнений модели с тем, чтобы обеспечить большее совпадение данных, рассчитанных по модели, с фактическими показателями. [25]
Принятие некоторых критических решений во всех случаях должно принадлежать человеку. Эти решения невозможно ввести в программу вычислительных машин. [26]
Медленный дрейф напряженности магнитного поля наиболее часто компенсируют путем запуска развертки аналого-цифрового преобразователя отчетливым сигналом резонанса, таким, например, как сигнал ТМС. Компенсацию дрейфа можно предусмотреть и в программе вычислительной машины, так чтобы перед сложением спектры совмещались друг с другом по совпадению их главных линий. Закрытые приборы настолько стабильны, что всего этого может не потребоваться, и развертку аналого-цифрового преобразователя достаточно будет синхронизовать с механической разверткой спектрометра. [27]
Система может быть рассчитана на выдачу данных о пределах, например успешная работа на высоте 75 000 м и более, или о диапазонах, например номинальная нагрузка в пределах от 0 90 до 1 2 вт. Можно вводить различные вариации, но это связано с усложнением программы вычислительной машины. [28]
Значительно большие возможности для использования ЗУ на магнитных лентах в вычислительных машинах и системах дает запись в зоны, размеры которых могут изменяться в широких пределах. Размер зоны может устанавливаться при решении той или иной задачи программой вычислительной машины. Число машинных слов, располагаемых в зоне, не должно превышать емкости ОЗУ, для того чтобы можно было переписывать информацию в ОЗУ из зоны на магнитной ленте. Следует отметить, что запись очень короткими зонами приводит к плохому использованию поверхности магнитного носителя, так как доля общей длины носителя, приходящаяся на промежутки между зонами, может быть весьма значительной. [29]
Для вычисления кривых зернового состава материала на различных стадиях измельчения были использованы функции измельчения, определенные методом радиоактивных индикаторов. Полученные результаты хорошо согласуются с экспериментальными значениями, принимая во внимание изменчивость данных по просеиванию и простоту программы вычислительной машины. Можно надеяться, что методы, описанные в этом исследовании, можно использовать на промышленных установках по измельчению и что такая работа будет полезна как для изготовителей измельчающих механизмов, так и для их потребителей. [30]
Страницы: 1 2 3 4